题目内容
设正实数x,y,z满足x2-3xy+9y2-z=0,则当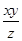 取得最大值时,
取得最大值时,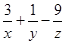 的最大值为( )
的最大值为( )
| A.1 | B.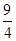 | C.-1 | D.3 |
A
解析试题分析:由题可知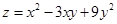
 分子分母同时除以xy,可以得到
分子分母同时除以xy,可以得到 x,y,z都是正实数,所以可以利用基本不等式有
x,y,z都是正实数,所以可以利用基本不等式有 所以
所以 ,当且仅当
,当且仅当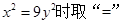 即
即 ,将
,将 代入
代入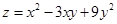 得
得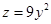
所以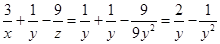 配方得,
配方得,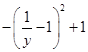 所以最大值是1.故答案是A.
所以最大值是1.故答案是A.
考点:基本不等式

练习册系列答案
相关题目
已知不等式 的解集为
的解集为 ,点
,点 在直线
在直线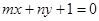 上,其中
上,其中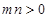 ,则
,则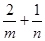 的最小值为( )
的最小值为( )
A.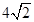 | B.8 | C.9 | D.12 |
设a,b是两个实数,且a≠b,① ②
② ,③
,③ 。上述三个式子恒成立的有( )
。上述三个式子恒成立的有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
函数 的最大值是( )
的最大值是( )
A. | B.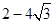 | C. | D. |
若正实数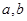 满足
满足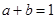 ,则
,则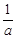 +
+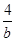 的最小值是( )
的最小值是( )
| A.4 | B.6 | C.8 | D.9 |
若 且
且 ,使不等式
,使不等式 ≥
≥ 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. ≤ ≤ | B. ≤ ≤ | C. ≥ ≥ | D. ≥ ≥ |
设 是正实数,以下不等式
是正实数,以下不等式
① 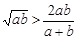 ,②
,② 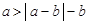 ,③
,③  ,④
,④  恒成立的序号为( )
恒成立的序号为( )
| A.①、③ | B.①、④ | C.②、③ | D.②、④ |
设 ,
,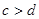 ,则下列不等式成立的是( )。
,则下列不等式成立的是( )。
A. | B. | C. | D. |
若两个正实数x,y满足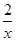 +
+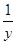 =1,并且x+2y>m2+2m恒成立,则实数m的取值范围是( )
=1,并且x+2y>m2+2m恒成立,则实数m的取值范围是( )
| A.(-∞,-2)∪[4,+∞) | B.(-∞,-4]∪[2,+∞) |
| C.(-2,4) | D.(-4,2) |