题目内容
设甲、乙两人每次射击命中目标的概率分别为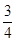 和
和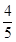 ,且各次射击相互独立,若按甲、乙、甲、乙、…的次序轮流射击,直到有一人击中目标就停止射击,则射击停止时,甲射击了两次的概率是 ( )
,且各次射击相互独立,若按甲、乙、甲、乙、…的次序轮流射击,直到有一人击中目标就停止射击,则射击停止时,甲射击了两次的概率是 ( )
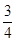 和
和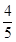 ,且各次射击相互独立,若按甲、乙、甲、乙、…的次序轮流射击,直到有一人击中目标就停止射击,则射击停止时,甲射击了两次的概率是 ( )
,且各次射击相互独立,若按甲、乙、甲、乙、…的次序轮流射击,直到有一人击中目标就停止射击,则射击停止时,甲射击了两次的概率是 ( )A.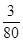 | B.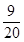 | C.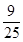 | D.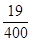 |
略
设A表示甲命中目标,B表示乙命中目标,则A、B相互独立,
停止射击时甲射击了两次包括两种情况:
①第一次射击甲乙都未命中,甲第二次射击时命中,
此时的概率P1=P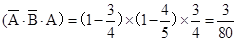 ,
,
②第一次射击甲乙都未命中,甲第二次射击未命中,而乙在第二次射击时命中,
此时的概率P2=P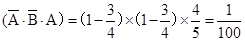 ,
,
故停止射击时甲射击了两次的概率P=P1+P2= ;
;
故选D.
停止射击时甲射击了两次包括两种情况:
①第一次射击甲乙都未命中,甲第二次射击时命中,
此时的概率P1=P
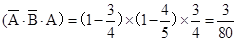 ,
,②第一次射击甲乙都未命中,甲第二次射击未命中,而乙在第二次射击时命中,
此时的概率P2=P
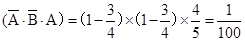 ,
,故停止射击时甲射击了两次的概率P=P1+P2=
 ;
;故选D.

练习册系列答案
相关题目



 ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为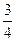 ,
,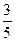 .
.
 的数学期望;
的数学期望; 中有
中有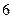 张卡片,其中
张卡片,其中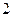 张写有数字
张写有数字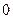 ,
,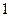 ,
,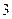 张写有数
张写有数 字
字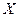 ,求
,求 求这二人都来自C科的概率.
求这二人都来自C科的概率.
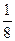
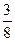
 部队立即前往甲地准备实施人工增雨作业,已知“人工增雨”高炮车Ⅰ号载有3枚“增雨炮弹”和1枚“增雨火箭”,通过炮击“积雨云”实施增雨,第一次击中积雨云只能使云层中的水分子凝聚,第二次击中同一积雨云才能成功增雨.如果需要第4次射击才使用“增雨火箭”,当增雨成功或者增雨弹用完才停止射击.每次射击相互独立,且用“增雨炮弹
部队立即前往甲地准备实施人工增雨作业,已知“人工增雨”高炮车Ⅰ号载有3枚“增雨炮弹”和1枚“增雨火箭”,通过炮击“积雨云”实施增雨,第一次击中积雨云只能使云层中的水分子凝聚,第二次击中同一积雨云才能成功增雨.如果需要第4次射击才使用“增雨火箭”,当增雨成功或者增雨弹用完才停止射击.每次射击相互独立,且用“增雨炮弹 ”击中积雨云的概率是
”击中积雨云的概率是 ,用“增雨火箭”击中积雨云的概率是
,用“增雨火箭”击中积雨云的概率是 .
.

 求不使用“增雨火箭”就能成功增雨的概率;
求不使用“增雨火箭”就能成功增雨的概率;