题目内容
已知t>0,关于x的方程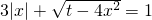 有相异实根的个数情况是
有相异实根的个数情况是
- A.0或1或2或3
- B.0或1或2或4
- C.0或2或3或4
- D.0或1或2或3或4
B
分析:由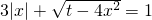 ,可得3|x|-1=-
,可得3|x|-1=-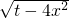 ,
,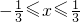 ,同时平方可得t-4x2=9x2-6|x|+1即t=13x2-6|x|+1,在同一坐标系中画出函数y=13x2-6|x|+1 (-
,同时平方可得t-4x2=9x2-6|x|+1即t=13x2-6|x|+1,在同一坐标系中画出函数y=13x2-6|x|+1 (- ≤x≤
≤x≤ )的图象和函数y=t 的图象如图数形结合可得结论.
)的图象和函数y=t 的图象如图数形结合可得结论.
解答: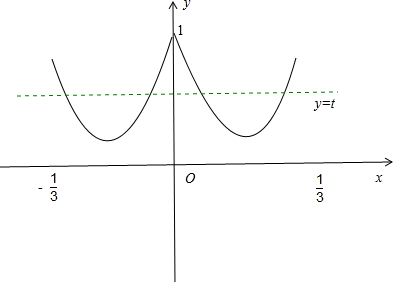 解:∵t>0,关于x的方程程
解:∵t>0,关于x的方程程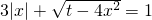
即3|x|-1=-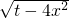 ,
,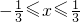
两边 同时平方可得,t-4x2=9x2-6|x|+1
∴t=13x2-6|x|+1
在同一坐标系中画出函数y=13x2-6|x|+1 (- ≤x≤
≤x≤ )的图象和函数y=t 的图象如图
)的图象和函数y=t 的图象如图
①t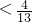 或t>1时,两函数的图象有0个交点
或t>1时,两函数的图象有0个交点
②当t=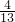 或
或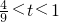 时,两函数的图象有2个交点
时,两函数的图象有2个交点
③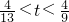 时,两函数的图象有4个交点
时,两函数的图象有4个交点
④t=1时,两函数的图象有1个交点
∴t>0,关于x的方程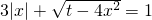 有相异实根的个数情况是o或1或2或4
有相异实根的个数情况是o或1或2或4
故选B
点评:本题主要考查图象法判断方程的实根个数,关键是画出两个函数的图象,属于基础题.
分析:由
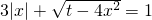 ,可得3|x|-1=-
,可得3|x|-1=-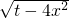 ,
,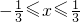 ,同时平方可得t-4x2=9x2-6|x|+1即t=13x2-6|x|+1,在同一坐标系中画出函数y=13x2-6|x|+1 (-
,同时平方可得t-4x2=9x2-6|x|+1即t=13x2-6|x|+1,在同一坐标系中画出函数y=13x2-6|x|+1 (- ≤x≤
≤x≤ )的图象和函数y=t 的图象如图数形结合可得结论.
)的图象和函数y=t 的图象如图数形结合可得结论.解答:
 解:∵t>0,关于x的方程程
解:∵t>0,关于x的方程程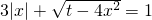
即3|x|-1=-
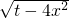 ,
,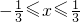
两边 同时平方可得,t-4x2=9x2-6|x|+1
∴t=13x2-6|x|+1
在同一坐标系中画出函数y=13x2-6|x|+1 (-
 ≤x≤
≤x≤ )的图象和函数y=t 的图象如图
)的图象和函数y=t 的图象如图①t
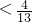 或t>1时,两函数的图象有0个交点
或t>1时,两函数的图象有0个交点②当t=
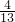 或
或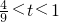 时,两函数的图象有2个交点
时,两函数的图象有2个交点③
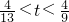 时,两函数的图象有4个交点
时,两函数的图象有4个交点④t=1时,两函数的图象有1个交点
∴t>0,关于x的方程
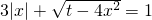 有相异实根的个数情况是o或1或2或4
有相异实根的个数情况是o或1或2或4故选B
点评:本题主要考查图象法判断方程的实根个数,关键是画出两个函数的图象,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则这个方程有相异实根的个数情况是 .
,则这个方程有相异实根的个数情况是 .