题目内容
已知t>0,关于x的方程 ,则这个方程有相异实根的个数情况是 .
,则这个方程有相异实根的个数情况是 .
【答案】分析:因为关于x的方程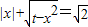 等号两边均为正数,所以方程等价于方程
等号两边均为正数,所以方程等价于方程 ,再转化为
,再转化为 的图象的交点问题,可通过在同一坐标系中做出函数
的图象的交点问题,可通过在同一坐标系中做出函数 ,的图象,通过判断图象交点个数来判断方程的相异实根根数.
,的图象,通过判断图象交点个数来判断方程的相异实根根数.
解答: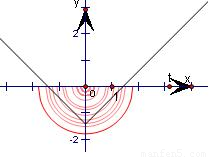 解:令
解:令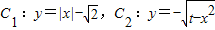 ,
,
由于y=|x|- =
=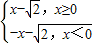 ,
,
方程 平方得:x2+y2=t,(y≤0),
平方得:x2+y2=t,(y≤0),
画出它们的图象,如图所示,一个是折线,一个是半个圆.
当圆心(0,0)到直线y=x-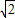 的距离等于半径时,
的距离等于半径时,
即 =
=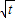 时,t=1;
时,t=1;
当圆经过点(0,- )时,02+(-
)时,02+(- )2=t,⇒t=2.
)2=t,⇒t=2.
利用数形结合知:当0<t<1或t>2时,方程无实数根;
当t=1时,方程有2个实数根;
当t=2时,方程有3个实数根;
当1<t<2时,方程有4个实数根.
综合,则这个方程有相异实根的个数情况是 2或3或4.
故答案为:0或2或3或4.
点评:本题主要考查图象法判断方程的实根个数,关键是画出两个函数的图象.
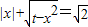 等号两边均为正数,所以方程等价于方程
等号两边均为正数,所以方程等价于方程 ,再转化为
,再转化为 的图象的交点问题,可通过在同一坐标系中做出函数
的图象的交点问题,可通过在同一坐标系中做出函数 ,的图象,通过判断图象交点个数来判断方程的相异实根根数.
,的图象,通过判断图象交点个数来判断方程的相异实根根数.解答:
 解:令
解:令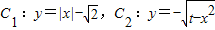 ,
,由于y=|x|-
 =
=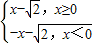 ,
,方程
 平方得:x2+y2=t,(y≤0),
平方得:x2+y2=t,(y≤0),画出它们的图象,如图所示,一个是折线,一个是半个圆.
当圆心(0,0)到直线y=x-
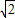 的距离等于半径时,
的距离等于半径时,即
 =
=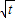 时,t=1;
时,t=1;当圆经过点(0,-
 )时,02+(-
)时,02+(- )2=t,⇒t=2.
)2=t,⇒t=2.利用数形结合知:当0<t<1或t>2时,方程无实数根;
当t=1时,方程有2个实数根;
当t=2时,方程有3个实数根;
当1<t<2时,方程有4个实数根.
综合,则这个方程有相异实根的个数情况是 2或3或4.
故答案为:0或2或3或4.
点评:本题主要考查图象法判断方程的实根个数,关键是画出两个函数的图象.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目