题目内容
（本小题满分12分）袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为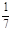
．现有甲、乙两人从袋中轮流摸取1个球，甲先取，乙后取，然后甲再取，
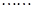，取后不放回，直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能的．求：
（1）则袋中原有白球的个数；
（2）取球2次终止的概率；
（3）甲取到白球的概率
【答案】
解：（1）（设袋中原有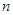
个白球，由题意知
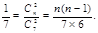
所以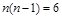
，解得
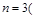舍去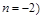
.即袋中原有３个白球. …………………4分
（2）记“取球2次终止”的事件为A．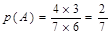 
…………………8分
（3）记“甲取到白球”的事件为B，“第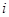
次取到的球是白球”的事件为
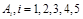，因为甲先取,所以甲只有可能在第1次、第3次和第5次取球，则 
.
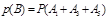因为事件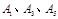
两两互斥，所以
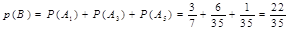…………………………………12分
【解析】略
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
