题目内容

17．在等比数列|an|中，若a1+a2+a3+a4+a5=3，a6+a7+a8+a9+a10=9，则a11+a12+a13+a14+a15=27．

分析 根据等比数列的性质求出公比即可．

解答 解：∵a1+a2+a3+a4+a5=3，a6+a7+a8+a9+a10=9，
∴（a1+a2+a3+a4+a5）q5=a6+a7+a8+a9+a10，
即3q5=9，即q5=3，
则a11+a12+a13+a14+a15=（a6+a7+a8+a9+a10）q5=9×3=27，
故答案为：27

点评 本题主要考查等比数列的性质的应用，根据条件求出公比是解决本题的关键．

练习册系列答案
相关题目
7．因式分解：mn（m-n）-m（n-m）2．
8．若圆C1：x2+y2=16与圆C2：（x-a）2+y2=1相切．则a的值为（　　）
A．±3B．±5C．3或5D．±3或±5
5．在等差数列{an}中，已知a1=23，公差d为整数，a6为正数，a7为负数，求a8．
12．已知函数f（x）=3x2-5x+2，求f（-$\sqrt{2}$），f（-a），f（a+3），f（a）
2．设集合A={（x，y）|y=x+1，x∈R}，B={（x，y）|y=-x2+2x+$\frac{3}{4}$，x∈R}，求A∩B．
9．求函数y=|x2+2x-3|的单调区间．
8．设{an}是各项均为正数的等比数列且a1+a2=2（$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$），a1+a2+a3=64（$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$）
（1）求数列{an}的通项公式；
（2）设bn=（an+$\frac{1}{{a}_{n}}$）2，求数列{bn}的前n项和为Tn．
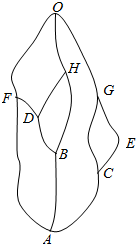9．观日出，赏瀑布，或是重温老别墅里的民国往事和《庐山恋》的柔美爱情，庐山每天都吸引大量的国内外游客，从山脚的A点徒步攀登到山顶O处的主景区，沿途风景秀丽，令人流连忘返，下图是一张登山的地图，若游客在每一个岔路口选择哪一条路线上山是等可能的（假定游客始终沿上山路线前进，不往下走，例如从F不能向D点走）
（1）求游客经过H点上到山顶的概率；
（2）在2014年国庆期间，每天大约有18000人至庐山旅游，给庐山的周边环境带来极大的压力，为保护环境，景区决定在E，F，H处设置环保宣传册发放点，每位游客到达E，F，H处领取材料的概率分别是$\frac{2}{3}$，$\frac{3}{5}$，$\frac{4}{5}$，则景区每天至少要提供多少册环保宣传材料才是合理的．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网