题目内容
10.设双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为e,右顶点为A,点Q(3a,0),若C上存在一点P,使得AP⊥PQ,则( )| A. | $e∈({1,\sqrt{2}})$ | B. | $e∈({\sqrt{2},\sqrt{3}})$ | C. | $e∈({1,\sqrt{3}})$ | D. | $e∈({\sqrt{2},+∞})$ |
分析 P(m,n),根据数量积为零算出(m-a)(3a-m)-n2=0,结合点P(m,n)在双曲线上消去n,得关于m的一元二次方程(m-a)(3a-m)-b2($\frac{{m}^{2}}{{a}^{2}}$-1)=0,此方程的一个根为a,而另一个根为大于a的实数,由此建立关于a、b、c不等式关系,化简整理即可得到离心率e的取值范围.
解答 解:设点P(m,n),可得$\overrightarrow{AP}$=(m-a,n),$\overrightarrow{PQ}$=(3a-m,-n),
∵AP⊥PQ,
∴$\overrightarrow{AP}$•$\overrightarrow{PQ}$=(m-a)(3a-m)-n2=0…(1)
又∵P(m,n)在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上,
∴得n2=b2($\frac{{m}^{2}}{{a}^{2}}$-1)…(2)
将(2)式代入(1)式,得(m-a)(3a-m)-b2($\frac{{m}^{2}}{{a}^{2}}$-1)=0,
化简整理,得-$\frac{{c}^{2}}{{a}^{2}}$m2+4am+c2-4a2=0,
此方程的一根为m1=a,另一根为m2=$\frac{4{a}^{3}-a{c}^{2}}{{c}^{2}}$.
∵点P是双曲线上异于右顶点A的一点,
∴$\frac{4{a}^{3}-a{c}^{2}}{{c}^{2}}$>a,得4a2>2c2,即e2<2,
由此可得双曲线的离心率e满足1<e<$\sqrt{2}$.
故选:A.
点评 本题给出双曲线上存在一点P,到A(a,0)和Q(3a,0)所张的角等于90°,求双曲线离心率的取值范围,着重考查了双曲线的简单几何性质和直线与双曲线关系等知识,属于中档题.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案| A. | y2=12x | B. | y2=6x | C. | y2=3x | D. | y2=24x |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 6 | B. | -6 | C. | 9 | D. | 12 |
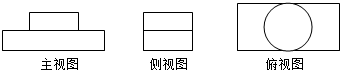
| A. |  | B. | 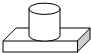 | C. | 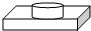 | D. | 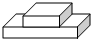 |
 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.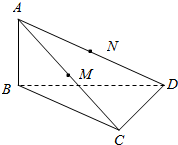 如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M、N分别是AC、AD的中点,BC⊥CD.