题目内容
已知函数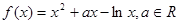
(1)若函数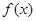 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数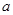 的取值范围;
的取值范围;
(2)令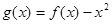 ,是否存在实数
,是否存在实数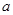 ,当
,当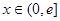 时,函数
时,函数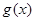 的最小值是3,若存在,求出
的最小值是3,若存在,求出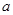 的取值;若不存在,说明理由.
的取值;若不存在,说明理由.
【答案】
(1)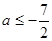 . (2)存在实数
. (2)存在实数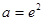 ,使得当
,使得当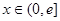 时,函数
时,函数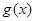 的最小值是3.
的最小值是3.
【解析】(1) 由题意得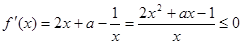 在[1,2]上恒成立,然后转化为
在[1,2]上恒成立,然后转化为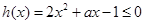 在[1,2]上恒成立,再利用二次函数的性质求解即可.
在[1,2]上恒成立,再利用二次函数的性质求解即可.
(2) 本小题属于存在性问题,应先假设存在实数 ,使
,使 有最小值3,然后利用导数求其最小值,然后建立关于a的方程求解即可验证是否存在
有最小值3,然后利用导数求其最小值,然后建立关于a的方程求解即可验证是否存在
(1)由题意得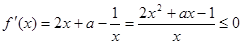 在[1,2]上恒成立,令
在[1,2]上恒成立,令
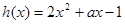 ,有
,有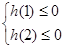 ,得
,得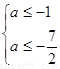 ,得
,得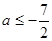 .
.
(2)假设存在实数 ,使
,使 有最小值3,由题知
有最小值3,由题知
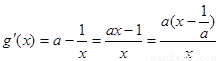 ,
,
当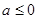 时,
时,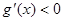 ,
,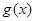 在
在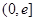 上单调递减,
上单调递减,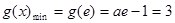 ,
,
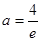 (舍去)
(舍去)
当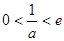 时,
时,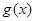 在
在 上单调递减,在
上单调递减,在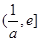 上单调递增,所以
上单调递增,所以
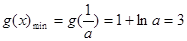 ,所以
,所以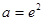 ,满足条件;
,满足条件;
当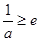 时,
时,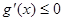 ,
,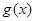 在
在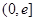 上单调递减,
上单调递减,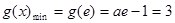 ,
,
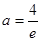 (舍去).
(舍去).
综上,存在实数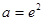 ,使得当
,使得当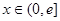 时,函数
时,函数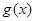 的最小值是3.
的最小值是3.

练习册系列答案
相关题目
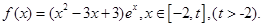
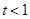 时,求函数
时,求函数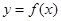 的单调区间;
的单调区间;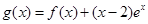 ,试问函数
,试问函数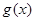 在
在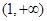 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.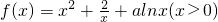 ,
,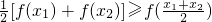 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.