题目内容
12.若函数y=cos(ωx+φ)(ω>0)的部分图象如图,则ω=( )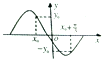
| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
分析 由条件利用函数y=Acos(ωx+φ)的周期为$\frac{2π}{ω}$=$\frac{2π}{3}$,可得ω的值.
解答 解:由函数的图象可得函数的周期为 $\frac{2π}{ω}$=2[(x0+$\frac{π}{3}$)-x0]=$\frac{2π}{3}$,求得ω=3,
故选:C.
点评 本题主要考查余弦函数的周期性,利用了函数y=Acos(ωx+φ)的周期为$\frac{2π}{ω}$,属于基础题.

练习册系列答案
相关题目
1.为调查某地区高三学生是否需要心理疏导,用简单随机抽样方法从该校调查了500位高三学生,结果如下:
(Ⅰ)估计该地区高三学生中,需要心理疏导的高三学生的百分比;
(Ⅱ)能否有99%的把握认为该地区高三学生是否需要心理疏导与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的抽样方法来调查估计该地区高三学生中,需要提供心理疏导的高三学生的比例?请说明理由.
附:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,
 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(Ⅱ)能否有99%的把握认为该地区高三学生是否需要心理疏导与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的抽样方法来调查估计该地区高三学生中,需要提供心理疏导的高三学生的比例?请说明理由.
附:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 10.828 |
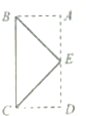 如图,矩形ABCD中,E为AD的中点,AB=1,BC=2,连接EB,EC,若△BEC绕直线AD旋转一周,则所形成的几何体的表面积为(4+2$\sqrt{2}$)π.
如图,矩形ABCD中,E为AD的中点,AB=1,BC=2,连接EB,EC,若△BEC绕直线AD旋转一周,则所形成的几何体的表面积为(4+2$\sqrt{2}$)π. 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,图象关于直线x=$\frac{π}{3}$对称.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,图象关于直线x=$\frac{π}{3}$对称.