题目内容
如图,三棱锥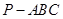 中,
中,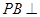 底面
底面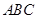 于
于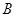 ,
,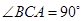 ,
,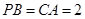 ,点
,点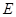 是
是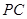 的中点.
的中点.

(1)求证:侧面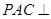 平面
平面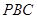 ;
;
(2)若异面直线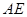 与
与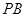 所成的角为
所成的角为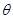 ,且
,且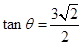 ,
,
求二面角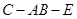 的大小.
的大小.
【答案】
(1)对于线面垂直的证明,主要是利用判定定理,然后结合这个条件来得到面面垂直的证明。
(2)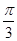
【解析】
试题分析:解:(1)∵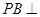 底面
底面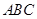 ,
, 平面
平面 ,
,
∴ 平面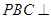 平面
平面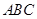 , 又∵
, 又∵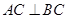 ,
,
平面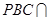 平面
平面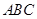
 , ∴
, ∴  平面
平面 3分
3分
而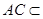 平面
平面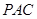 ∴侧面
∴侧面 平面
平面 .
5分
.
5分
(2)取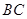 的中点
的中点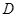 ,则
,则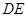 是
是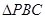 的中位线
的中位线
故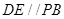 ,所以
,所以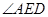 就是异面直线
就是异面直线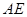 与
与 所成的角
所成的角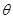 , 7分
, 7分
设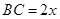 ,则在
,则在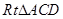 中,
中,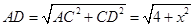 ,
,
在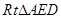 中,
中,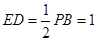 ,∴
,∴ 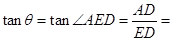
 ,
,
而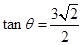 ,∴
,∴  ,即
,即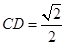 .
9分
.
9分
过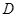 作
作 于点
于点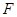 ,连
,连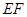 . ∵
. ∵
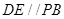 ,
,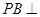 底面
底面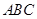
∴ 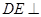 底面
底面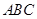 ,从而
,从而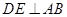 ,又∵
,又∵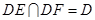 ,
,
∴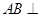 平面
平面 ,从而
,从而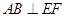 ,
,
所以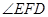 就是二面角
就是二面角 的平面角. 11分
的平面角. 11分
由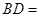
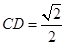 ,得
,得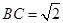 ,
由
,
由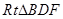 ∽
∽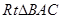 ,
,
可得 ,即
,即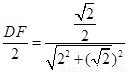 解得
解得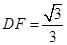 ,
,
在 中,
中, ,所以
,所以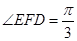 ,
,
故二面角 的大小为
的大小为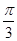 .
14分
.
14分
解法2:如图,以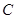 为原点,以
为原点,以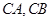 分别为
分别为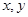 轴建立直角坐标系.
轴建立直角坐标系.

设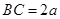 ,则
,则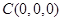 ,
,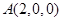 ,
,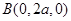 ,
,
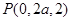 ,从而
,从而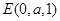 .
.
∴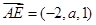 ,
, , 7分
, 7分
∵异面直线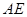 与
与 所成的角为
所成的角为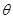 ,且
,且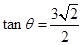 ,
,
∴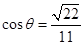 ,
,
又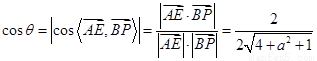 ,
,
从而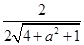
 ,解得
,解得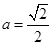 ...
9分
...
9分
∴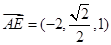 ,
,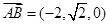 ,
, ,
,
设平面 的法向量为
的法向量为 ,则由
,则由
得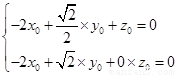 , 令
, 令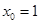 ,得
,得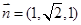 .
11分
.
11分
又平面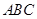 的法向量为
的法向量为 , 12分
, 12分
∴
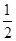 ,∴
,∴  ,
,
所以二面角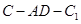 的大小为
的大小为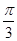 .
14分
.
14分
考点:面面垂直,二面角
点评:主要是考查了空间几何体中垂直的证明以及异面直线的角和二面角的平面角的借助于向量来求解,属于中档题。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图,三棱锥
如图,三棱锥
 中,
中, 底面
底面 ,
, ,
, ,
, 为
为 的中点,点
的中点,点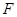 在
在 上,且
上,且 .
.
 平面
平面 ;
;  与平面
与平面 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值. 中,
中, ^底面
^底面 ,若底面
,若底面
 ,若
,若 是
是 的中点,
的中点,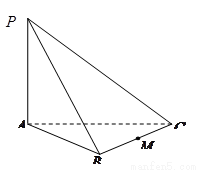
 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).