题目内容
在等差数列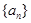 中,若任意两个不等的正整数
中,若任意两个不等的正整数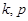 ,都有
,都有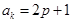 ,
,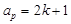 ,设数列
,设数列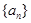 的前
的前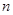 项和为
项和为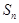 ,若
,若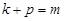 ,则
,则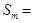 (结果用
(结果用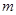 表示)。
表示)。
【答案】
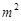
【解析】解:设公差为d,∵ak=2p+1=a1+(k-1)d (1),ap=2k+1=a1+(p-1)d (2),
由(1)-(2)可得d=-2.
故有 a1+(k-1)(-2)=a1+(p-1)(-2),∴a1-2(k-1)=2p+1,∴a1=2p+1+2(k-1)=2(p+k)-1=2m-1.
Sm=ma1+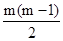 d=m(2m-1)+
d=m(2m-1)+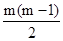 •(-2)=m2,故答案为 m2
•(-2)=m2,故答案为 m2

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
以下命题中正确的是( )
A、若x∈R且x≠0,则x+
| ||
| B、在△ABC中,若sin2A=sin2B,则△ABC是等腰三角形 | ||
| C、对等差数列{an}的前n项和Sn,若对任意正整数n都有Sn+1>Sn,则an+1>an对任意正整数n恒成立 | ||
| D、a=3是直线ax+2y+3a=0与直线3x+(a-1)y=a-7平行且不重合的充要条件 |
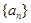 中,若任意两个不等的正整数
中,若任意两个不等的正整数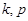 ,都有
,都有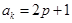 ,
,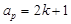 ,设数列
,设数列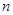 项和为
项和为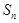 ,若
,若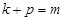 ,则
,则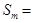 (结果用
(结果用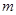 表示)。
表示)。