题目内容
已知定点A为(2,0),圆x2+y2=1上有一个动点Q,若线段AQ的中点为点P,则动点P的轨迹是 .
分析:设出动点P、Q的坐标,利用线段AQ的中点为点P,确定坐标之间的关系,利用Q是圆x2+y2=1上的动点,即可求得方程,从而可得动点P的轨迹.
解答:解:设P的坐标为(x,y),Q(a,b),则
∵定点A为(2,0),线段AQ的中点为点P,
∴
∴a=2x-2,b=2y
∵Q是圆x2+y2=1上的动点
∴a2+b2=1
∴(2x-2)2+(2y)2=1
∴(x-1)2+y2=
∴动点P的轨迹是以(1,0)为圆心,半径长为
的圆
故答案为:以(1,0)为圆心,半径长为
的圆.
∵定点A为(2,0),线段AQ的中点为点P,
∴
|
∴a=2x-2,b=2y
∵Q是圆x2+y2=1上的动点
∴a2+b2=1
∴(2x-2)2+(2y)2=1
∴(x-1)2+y2=
| 1 |
| 4 |
∴动点P的轨迹是以(1,0)为圆心,半径长为
| 1 |
| 2 |
故答案为:以(1,0)为圆心,半径长为
| 1 |
| 2 |
点评:本题考查轨迹方程,考查代入法的运用,解题的关键是确定动点坐标之间的关系,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 已知定点A(-2,0),动点B是圆
已知定点A(-2,0),动点B是圆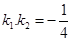 ,其中k1、k2分别表示直线AP、BP的斜率.
,其中k1、k2分别表示直线AP、BP的斜率.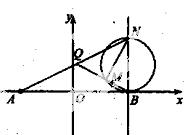
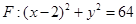 (F为圆心)上一点,线段AB的垂直平分线交BF于P.w.w.w.zxxk.c.o.m
(F为圆心)上一点,线段AB的垂直平分线交BF于P.w.w.w.zxxk.c.o.m
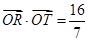 (O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(O为原点).若存在,求直线l的方程;若不存在,请说明理由.