题目内容
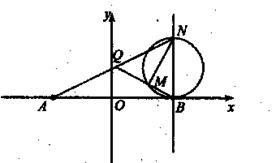
已知定点A（－2，0），动点B是圆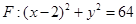
（F为圆心）上一点，线段AB的垂直平分线交BF于P．w.w.w.zxxk.c.o.m
（I）求动点P的轨迹方程；
（II）是否存在过点E（0，－4）的直线l交P点的轨迹于点R，T， 且满足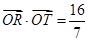
（O为原点）．若存在，求直线l的方程；若不存在，请说明理由．
【答案】
(1) 
(2) 
【解析】解：（1）由题意得|PA|=|PB|且|PB|+|PF|=r=8. 故|PA|+|PF|=8>|AF|=4
∴P点轨迹为以A、F为焦点的椭圆.……………3分
设椭圆方程为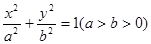
. ……………………… 6分
（2）假设存在满足题意的直线L.易知当直线的斜率不存在时,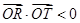 
不满足题意.
故设直线L的斜率为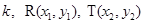
.
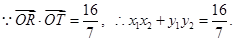………………………………7分
练习册系列答案
阅读快车系列答案
相关题目
（本题满分14分）
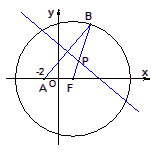已知定点A（－2，0），动点B是圆
（F为圆心）上一点，线段AB的垂直平分线交BF于P．
（1）求动点P的轨迹方程；
|
（O为原点）．若存在，求直线l的方程；若不存在，请说明理由． 
已知定点A（－2，0），动点B是圆
（F为圆心）上一点，线段AB的垂直平分线交BF于P．
（O为原点）．若存在，求直线l的方程；若不存在，请说明理由．
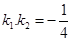，其中k1、k2分别表示直线AP、BP的斜率．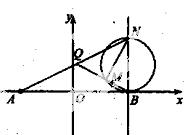
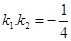，其中k1、k2分别表示直线AP、BP的斜率．