题目内容
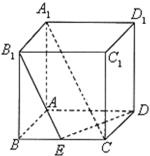 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,平面B1ED交A1D1于F
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,平面B1ED交A1D1于F(1)指出F在A1D1上的位置,并证明.
(2)求直线A1C与B1F所成角的余弦值.
分析:(1)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系A-xyz,求出
与
,再根据向量平行建立等量关系,从而求出点F的位置;
(2)先分别求出直线A1C与B1F的向量坐标,求出向量
与
的夹角余弦值,再根据异面直线所成角的范围求出直线A1C与B1F所成角的余弦值即可.
| B1F |
| ED |
(2)先分别求出直线A1C与B1F的向量坐标,求出向量
| A1C |
| B1F |
解答: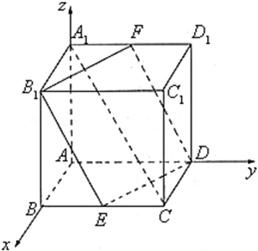 解:(1)以A为原点建立空间直角坐标系A-xyz.
解:(1)以A为原点建立空间直角坐标系A-xyz.
∵面ABCD∥面A1B1C1D1,面B1EDF∩面A1B1C1D1=B1F,
面B1EDF∩面ABCD=DE
∴B1F∥DE
又∵D(0,1,0),E(1,
,0),B1(1,0,1)
设F(0,y,1),则
=(-1,y,0),
=(-1,
,0)
∴(-1)•
-y•(-1)=0即y=
∴|
| =
=
|
|
∴F为A1D1的中点
(2)A1(0,0,1),C(1,1,0),则
=(1,1,-1),cos<
,
>=-
∴A1C与B1F所成角的余弦值为
(12分)
 解:(1)以A为原点建立空间直角坐标系A-xyz.
解:(1)以A为原点建立空间直角坐标系A-xyz.∵面ABCD∥面A1B1C1D1,面B1EDF∩面A1B1C1D1=B1F,
面B1EDF∩面ABCD=DE
∴B1F∥DE
又∵D(0,1,0),E(1,
| 1 |
| 2 |
设F(0,y,1),则
| B1F |
| ED |
| 1 |
| 2 |
∴(-1)•
| 1 |
| 2 |
| 1 |
| 2 |
∴|
| A1F |
| 1 |
| 2 |
| 1 |
| 2 |
| A1D1 |
∴F为A1D1的中点
(2)A1(0,0,1),C(1,1,0),则
| A1C |
| A1C |
| B1F |
| ||
| 5 |
∴A1C与B1F所成角的余弦值为
| ||
| 15 |
点评:本小题主要考查异面直线所成的角,以及空间向量,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
