题目内容
①在极坐标系中,点A(2,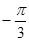 )到直线
)到直线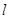 :
: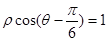 的距离为
的距离为
②(不等式选讲选做题) 设函数f(x)=|x-2|+x,g(x)=|x+1|,则g(x)<f(x)成立时x的取值范围
【答案】
(1)1;(2)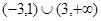
【解析】
试题分析:把点A的极坐标化为直角坐标,把直线的极坐标方程化为直角坐标方程,利用点到直线的距离公式求出A到直线的距离,由于点A(2,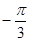 )的直角坐标为(1,-
)的直角坐标为(1,-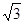 ),而直线
),而直线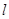 :
: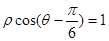 为x
为x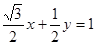 ,那么结合点到直线的距离公式可知为d=1
,那么结合点到直线的距离公式可知为d=1
(2)根据
设函数f(x)=|x-2|+x,g(x)=|x+1|,则g(x)<f(x)成立时,则即为|x+1|<|x-2|+x,去掉绝对值符号可知,不等式的解集为x>2,得到x>3,x<-1时,得到-3<x<-1,当-1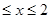 时,则可知解集为-1<x<1,故可知不等式的解集
时,则可知解集为-1<x<1,故可知不等式的解集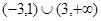
考点:极坐标方程化为直角坐标方程
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,以及绝对值不等式的求解,属于基础题.

练习册系列答案
相关题目
在极坐标系中,点A(1,π)到直线ρcosθ=2的距离是( )
| A、1 | B、2 | C、3 | D、4 |