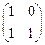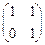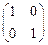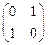题目内容
对于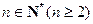 ,定义一个如下数阵:
,定义一个如下数阵:
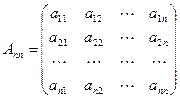
其中对任意的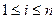 ,
,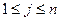 ,当
,当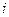 能整除
能整除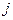 时,
时,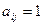 ;当
;当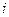 不能整除
不能整除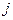 时,
时,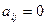 .设
.设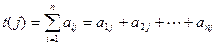 .
.
(Ⅰ)当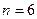 时,试写出数阵
时,试写出数阵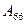 并计算
并计算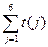 ;
;
(Ⅱ)若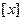 表示不超过
表示不超过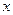 的最大整数,求证:
的最大整数,求证: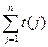
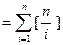 ;
;
(Ⅲ)若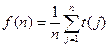 ,
,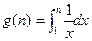 ,求证:
,求证: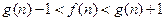 .
.
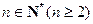 ,定义一个如下数阵:
,定义一个如下数阵: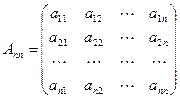
其中对任意的
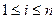 ,
,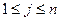 ,当
,当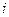 能整除
能整除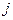 时,
时,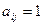 ;当
;当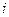 不能整除
不能整除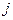 时,
时,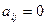 .设
.设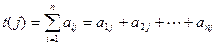 .
.(Ⅰ)当
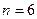 时,试写出数阵
时,试写出数阵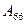 并计算
并计算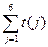 ;
;(Ⅱ)若
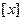 表示不超过
表示不超过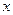 的最大整数,求证:
的最大整数,求证: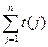
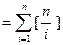 ;
;(Ⅲ)若
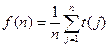 ,
,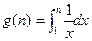 ,求证:
,求证: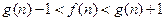 .
. (Ⅰ)解:依题意可得,
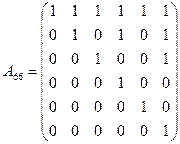 .
.
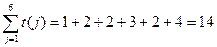 .
.
(Ⅱ)解:由题意可知,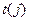 是数阵
是数阵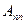 的第
的第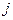 列的和,
列的和,
因此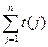 是数阵
是数阵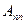 所有数的和.
所有数的和.
而数阵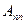 所有数的和也可以考虑按行相加.
所有数的和也可以考虑按行相加.
对任意的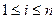 ,不超过
,不超过 的倍数有
的倍数有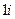 ,
,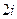 ,…,
,…,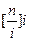 .
.
因此数阵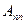 的第
的第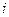 行中有
行中有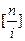 个1,其余是
个1,其余是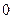 ,即第
,即第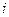 行的和为
行的和为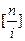 .
.
所以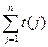
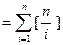 .
.
(Ⅲ)证明:由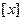 的定义可知,
的定义可知,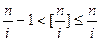 ,
,
所以 .
.
所以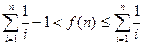 .
.
考查定积分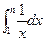 ,
,
将区间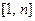 分成
分成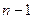 等分,则
等分,则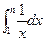 的不足近似值为
的不足近似值为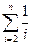 ,
,
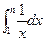 的过剩近似值为
的过剩近似值为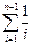 .
.
所以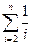
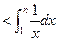
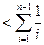 .
.
所以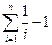

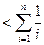 .
.
所以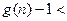
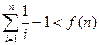
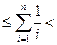
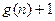 .
.
所以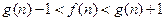 .
.
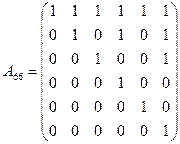 .
.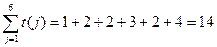 .
.(Ⅱ)解:由题意可知,
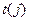 是数阵
是数阵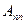 的第
的第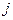 列的和,
列的和,因此
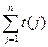 是数阵
是数阵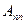 所有数的和.
所有数的和.而数阵
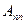 所有数的和也可以考虑按行相加.
所有数的和也可以考虑按行相加.对任意的
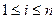 ,不超过
,不超过 的倍数有
的倍数有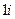 ,
,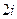 ,…,
,…,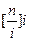 .
.因此数阵
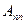 的第
的第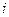 行中有
行中有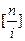 个1,其余是
个1,其余是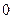 ,即第
,即第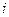 行的和为
行的和为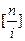 .
.所以
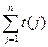
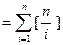 .
.(Ⅲ)证明:由
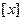 的定义可知,
的定义可知,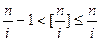 ,
,所以
 .
.所以
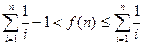 .
.考查定积分
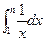 ,
,将区间
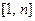 分成
分成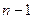 等分,则
等分,则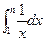 的不足近似值为
的不足近似值为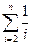 ,
,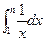 的过剩近似值为
的过剩近似值为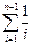 .
.所以
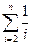
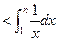
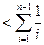 .
.所以
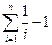

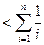 .
.所以
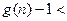
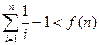
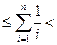
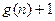 .
.所以
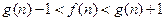 .
.略

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
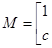
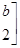 有特征值
有特征值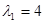 及对应的一个特征向量
及对应的一个特征向量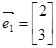 ,求曲线
,求曲线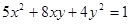 在
在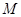 的作用下的新曲线方程.
的作用下的新曲线方程.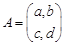 ,其中每一个数字称为二阶矩阵的元素,又记二阶矩阵乘法
,其中每一个数字称为二阶矩阵的元素,又记二阶矩阵乘法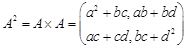 ,请观察二阶矩阵乘法的规律,写出
,请观察二阶矩阵乘法的规律,写出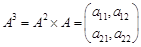 中的元素
中的元素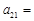 __________.
__________.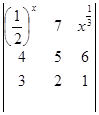 中,第3行第2列的元素的代数余子式记作
中,第3行第2列的元素的代数余子式记作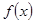 ,
,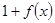 的零点属于区间 ( )
的零点属于区间 ( )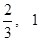 );
);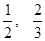 );
);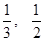 );
);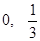 );
);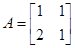 ,向量
,向量 ,求向量
,求向量 ,使得
,使得 .
.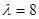 及对应的一个特征向量
及对应的一个特征向量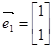 ,并且矩阵M对应的变换将点(-1,2)变换成(-2,4)。
,并且矩阵M对应的变换将点(-1,2)变换成(-2,4)。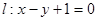 在矩阵M的作用下的直线
在矩阵M的作用下的直线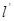 的方程。
的方程。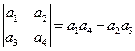 ,将函数
,将函数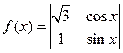 的图象向左平移
的图象向左平移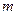 个单位(
个单位(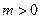 ),若所得图象对应的函数为偶函数,则
),若所得图象对应的函数为偶函数,则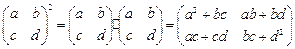 . 则
. 则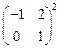 为
为