题目内容
若椭圆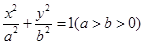 的左、右焦点分别为F1,F2,椭圆的离心率为
的左、右焦点分别为F1,F2,椭圆的离心率为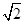 :2.(1)过点C(-1,0)且以向量
:2.(1)过点C(-1,0)且以向量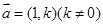 为方向向量的直线
为方向向量的直线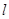 交椭圆于不同两点A、B,若
交椭圆于不同两点A、B,若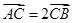 ,则当△OAB的面积最大时,求椭圆的方程。
,则当△OAB的面积最大时,求椭圆的方程。
(2)设M,N为椭圆上的两个动点,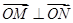 ,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
【答案】
(1)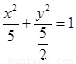 (2)
(2)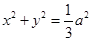
【解析】
试题分析:(1)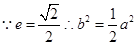 ,设椭圆的方程为
,设椭圆的方程为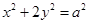
依题意,直线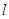 的方程为:
的方程为:
由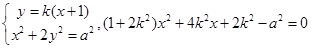
设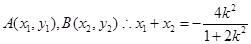
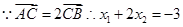
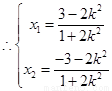
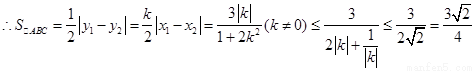
当且仅当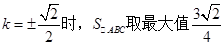
此时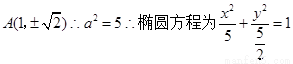
(2)设点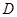 的坐标为
的坐标为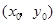 .
.
当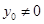 时,由
时,由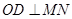 知,直线
知,直线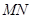 的斜率为
的斜率为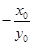 ,所以直线
,所以直线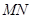 的方程为
的方程为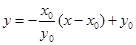 ,或
,或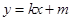 ,其中
,其中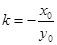 ,
,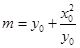 .
.
点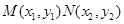 的坐标满足方程组
的坐标满足方程组
得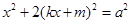 ,整理得
,整理得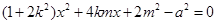 ,
,
于是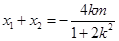 ,
,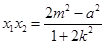 .
.
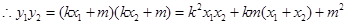
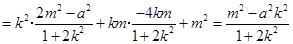 .
.
由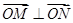 知
知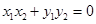 .
.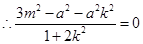 ,
,
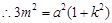 将
将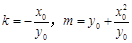 代入上式,整理得
代入上式,整理得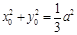 .
.
当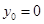 时,直线
时,直线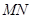 的方程为
的方程为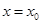 ,
,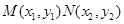 的坐标满足方程组
的坐标满足方程组
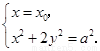 所以
所以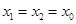 ,
,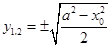 .
.
由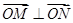 知
知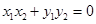 ,即
,即 ,
,
解得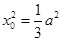 .
.
这时,点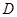 的坐标仍满足
的坐标仍满足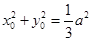 .
.
综上,点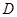 的轨迹方程为
的轨迹方程为 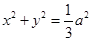
考点:直线与圆锥曲线的综合问题;椭圆的标准方程
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,抛物线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目


 (本小题满分12分) 已知椭圆
(本小题满分12分) 已知椭圆
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,
, 是椭圆右准线上的一点,线段
是椭圆右准线上的一点,线段 的垂直平分线过点
的垂直平分线过点 :
: 按向量
按向量 平移后的直线是
平移后的直线是 ,直线
,直线 :
: 按向量
按向量 平移后的直线是
平移后的直线是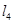 (其中
(其中 )。
)。 的取值范围。
的取值范围。 时,求椭圆的方程。
时,求椭圆的方程。 、
、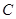 两点,
两点, 、
、 两点。求四边形ABCD面积
两点。求四边形ABCD面积 的取值范围。
的取值范围。