题目内容
8.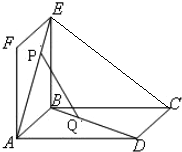 如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.
如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.
分析 过点M作MP⊥AB,交AB与点M,连接MQ,证明平面PMQ∥平面BCE,再证明PQ∥平面BCE即可.
解答 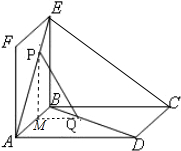 解:过点P作PM⊥AB,交AB与点M,连接MQ,如图所示,
解:过点P作PM⊥AB,交AB与点M,连接MQ,如图所示,
∴MP∥EB,
∴$\frac{AP}{PE}$=$\frac{AM}{MB}$;
又∵AE=BD,AP=DQ,
∴PE=BQ,
∴$\frac{AM}{MB}$=$\frac{DQ}{BQ}$,
∴MQ∥BC;
又∵BC?平面BCE,MQ?平面BCE,
∴MQ∥平面BCE,
同理,PM∥平面BCE;
又PM∩MQ=M,PM?平面PMQ,MQ?平面PMQ,
∴平面PMQ∥平面BCE;
∵PQ?平面PMQ,
∴PQ∥平面BCE.
点评 本题考查了直线与平面平行的判定问题,解题时应先证明面面平行,再证明线面平行,是中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
18.已知函数g(x)=$\frac{1}{3}$x3+2x-m+$\frac{m}{x}$(m>0)是[1,+∞)上的增函数.当实数m取最大值时,若存在点Q,使得过点Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
| A. | (0,-3) | B. | (2,-3) | C. | (0,0) | D. | (0,3) |
11.若i是虚数单位,Z的共轭复数$\overline{Z}$,复数z=$\frac{-1+3i}{1+2i}$,则$\overline Z$在复平面对应的点为( )
| A. | (5,5) | B. | (5,-5) | C. | (1,1) | D. | (1,-1) |
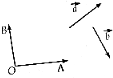 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$和$\overrightarrow{OA}$,$\overrightarrow{OB}$.求作:
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$和$\overrightarrow{OA}$,$\overrightarrow{OB}$.求作: