题目内容
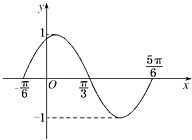
【题目】已知抛物线E：y2=2px（p＞0）的准线与x轴交于点K，过点K作圆（x﹣5）2+y2=9的两条切线，切点为M，N，|MN|=3 
（1）求抛物线E的方程；
（2）设A，B是抛物线E上分别位于x轴两侧的两个动点，且 
（其中O为坐标原点）．
①求证：直线AB必过定点，并求出该定点Q的坐标；
②过点Q作AB的垂线与抛物线交于G，D两点，求四边形AGBD面积的最小值．
【答案】
（1）解：由已知可得K（﹣ 
，0），圆C：（x﹣5）2+y2=9的圆心C（5，0），半径r=3．
设MN与x轴交于R，由圆的对称性可得|MR|= 
于是|CR|= 
，
即有|CK|= 
=6，
即有5+ =6，解得p=2，则抛物线E的方程为y2=4x
（2）证明①：设直线AB：x=my+t，A（ 
，y1），B（ 
，y2），
联立抛物线方程可得y2﹣4my﹣4t=0，
y1+y2=4m，y1y2=﹣4t，
，即有 +y1y2= 
，
解得y1y2=﹣18或2（舍去），
即﹣4t=﹣18，解得t= ．
则有AB恒过定点Q（ ，0）；
②解：由①可得|AB|= 
|y2﹣y1|= 
，
同理|GD|= 
，
则四边形AGBD面积S= 
|AB||GD|=4 
，
令m2+ 
=μ（μ≥2），则S=4 
是关于μ的增函数，
则当μ=2时，S取得最小值，且为88．
当且仅当m=±1时，四边形AGBD面积的最小值为88
【解析】（1）求得K的坐标，圆的圆心和半径，运用对称性可得MR的长，由勾股定理和锐角的三角函数，可得CK=6，再由点到直线的距离公式即可求得p=2，进而得到抛物线方程；（2）①设出直线方程，联立抛物线方程，运用韦达定理和向量的数量积的坐标表示，化简整理，即可得到定点Q；
②运用弦长公式和四边形的面积公式，换元整理，结合基本不等式，即可求得最小值．
教材全解字词句篇系列答案【题目】第 
届夏季奥林匹克运动会将于2016年8月5日 
21日在巴西里约热内卢举行．下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据（单位：枚）．
| 第31届里约 | 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 |
中国 | 26 | 38 | 51 | 32 | 28 |
俄罗斯 | 19 | 24 | 24 | 27 | 32 |
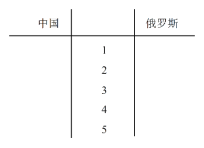
（1）根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图，并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度（不要求计算出具体数值，给出结论即可）；
（2）下表是近五届奥运会中国代表团获得的金牌数之和 
（从第 
届算起，不包括之前已获得的金牌数）随时间 
（时间代号）变化的数据：
届 | 27 | 28 | 29 | 30 | 31 |
时间代号(x) | 1 | 2 | 3 | 5 | |
金牌数之和(y枚) | 28 | 60 | 111 | 149 | 175 |
作出散点图如下：
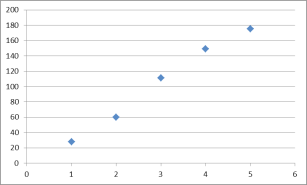
①由图中可以看出，金牌数之和 与时间代号 之间存在线性相关关系，请求出 关于 的线性回归方程；
②利用①中的回归方程，预测2020年第32届奥林匹克运动会中国代表团获得的金牌数．
参考数据：
，
，
．
附：对于一组数据 
，
，
，
，其回归直线
的斜率的最小二乘估计为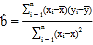
．
