题目内容
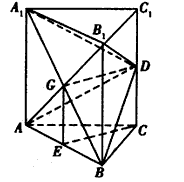
如图所示，正三棱柱ABC-A1B1C1的棱长均为a，D、E分别为C1C与AB的中点，A1B交AB1于G。
（1）求证：A1B⊥AD；
（2）求证：CE∥平面AB1D。
（2）求证：CE∥平面AB1D。
| 证明：（1）连接A1D，BD， ∵三棱柱ABC-A1B1C1是棱长均为a的正三棱柱， ∴A1ABB1为正方形， ∴A1B⊥AB1， ∵D是C1C的中点， ∴△A1C1D△BCD， ∴A1D=BD， ∵G是A1B中点， ∴A1B⊥DG， 又∵DG∩AB1=G， ∴A1B⊥平面AB1D， 又∵AD  平面AB1D， ∴A1B⊥AD； （2）连接GE，GD， ∵EG//A1A， ∴GE⊥平面ABC， ∵DC⊥平面ABC， ∴GE//DC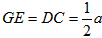， ∵  ∴四边形GECD为平行四边形， ∴EC∥GD， 又∵EC 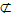 平面AB1D，DG 平面AB1D，∴EC//平面AB1D。 |
 |
练习册系列答案
相关题目
如图所示，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是
的底面边长为a，点M在BC上，
是以点M为直角顶点的等腰直角三角形。
的距离；
的大小。
，D是AC的中点．
，D是AC的中点．