题目内容
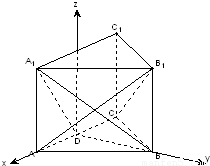
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是 ,D是AC的中点.
,D是AC的中点.(Ⅰ)求证:B1C∥平面A1BD;
(Ⅱ)求二面角A1-BD-A的大小;
(Ⅲ)求点A到平面A1BD的距离.

【答案】分析:(Ⅰ)设AB1与A1B相交于点P,连接PD,则P为AB1中点,由此能够证明B1C∥平面A1BD.
(Ⅱ)法一:由正三棱柱ABC-A1B1C1中D是AC的中点,知BD⊥AC,由平面AA1C1C⊥平面ABC,知BD⊥平面AA1C1C,故BD⊥A1D,∠A1DA为二面角A1-BD-A的平面角,由此能求出二面角A1-BD-A的大小.
(Ⅱ)法二:建立空间直角坐标系,利用向量法能求出二面角A1-BD-A的大小.
(Ⅲ)法一:由(Ⅱ)知BD⊥AC、BD⊥A1D,设点A到平面A1BD的距离为d,利用等积法能求出点A到平面A1BD的距离.
(Ⅲ)法二:由(Ⅱ)得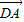 =(1,0,0),n=(
=(1,0,0),n=(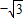 ,0,1),利用向量法能求出点A到平面A1BD的距离.
,0,1),利用向量法能求出点A到平面A1BD的距离.
解答: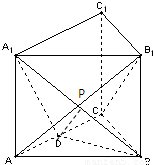 解:(Ⅰ)证明:设AB1与A1B相交于点P,连接PD,
解:(Ⅰ)证明:设AB1与A1B相交于点P,连接PD,
则P为AB1中点,
∵D为AC中点,
∴PD∥B1C.
又∵PD?平面A1BD,
∴B1C∥平面A1BD.…(4分)
(Ⅱ)解法一:由正三棱柱ABC-A1B1C1中D是AC的中点,
知BD⊥AC,
又∵平面AA1C1C⊥平面ABC,
∴BD⊥平面AA1C1C,∴BD⊥A1D,
故∠A1DA为二面角A1-BD-A的平面角,
又AD⊥A1A,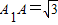 ,AD=1,
,AD=1,
∴∠A1DA=60°,即二面角A1-BD-A的大小为60°.…(8分)
(Ⅱ)解法二:如图建立空间直角坐标系,
则D(0,0,0),A(1,0,0),A1(1,0,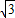 ),
),
B(0,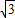 ,0),B1(0,
,0),B1(0,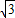 ,
,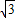 ),
),
∴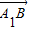 =(-1,
=(-1,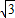 ,-
,-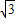 ),
),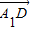 =(-1,0,-
=(-1,0,-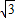 ),
),
设平面A1BD的法向量为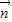 =(x,y,z),
=(x,y,z),
则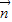
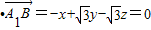
 ,
,
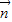
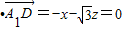
则有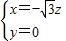 ,令z=1,得
,令z=1,得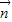 =(
=(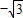 ,0,1)
,0,1)
由题意,知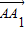 =(0,0,
=(0,0,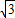 )是平面ABD的一个法向量.
)是平面ABD的一个法向量.
设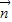 与
与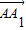 所成角为θ,
所成角为θ,
则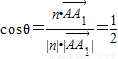 ,∴
,∴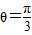 ,
,
∴二面角A1-BD-A的大小是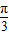 …(8分)
…(8分)
(Ⅲ)解法一:由(Ⅱ)知BD⊥AC、BD⊥A1D,
设点A到平面A1BD的距离为d,
∴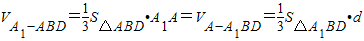 ,
,
故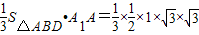
=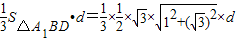
解得: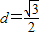 ,
,
即点A到平面A1BD的距离为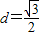 .…(12分)
.…(12分)
(Ⅲ)解法二:由(Ⅱ)已知,
得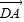 =(1,0,0),
=(1,0,0),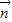 =(
=(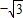 ,0,1)
,0,1)
则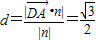
即点A到平面A1BD的距离为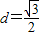 .…(12分)
.…(12分)
点评:本题考查直线与平面平行、二面角、点到平面的距离的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.
(Ⅱ)法一:由正三棱柱ABC-A1B1C1中D是AC的中点,知BD⊥AC,由平面AA1C1C⊥平面ABC,知BD⊥平面AA1C1C,故BD⊥A1D,∠A1DA为二面角A1-BD-A的平面角,由此能求出二面角A1-BD-A的大小.
(Ⅱ)法二:建立空间直角坐标系,利用向量法能求出二面角A1-BD-A的大小.
(Ⅲ)法一:由(Ⅱ)知BD⊥AC、BD⊥A1D,设点A到平面A1BD的距离为d,利用等积法能求出点A到平面A1BD的距离.
(Ⅲ)法二:由(Ⅱ)得
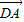 =(1,0,0),n=(
=(1,0,0),n=(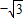 ,0,1),利用向量法能求出点A到平面A1BD的距离.
,0,1),利用向量法能求出点A到平面A1BD的距离.解答:
 解:(Ⅰ)证明:设AB1与A1B相交于点P,连接PD,
解:(Ⅰ)证明:设AB1与A1B相交于点P,连接PD,则P为AB1中点,
∵D为AC中点,
∴PD∥B1C.
又∵PD?平面A1BD,
∴B1C∥平面A1BD.…(4分)
(Ⅱ)解法一:由正三棱柱ABC-A1B1C1中D是AC的中点,
知BD⊥AC,
又∵平面AA1C1C⊥平面ABC,
∴BD⊥平面AA1C1C,∴BD⊥A1D,
故∠A1DA为二面角A1-BD-A的平面角,
又AD⊥A1A,
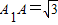 ,AD=1,
,AD=1,∴∠A1DA=60°,即二面角A1-BD-A的大小为60°.…(8分)
(Ⅱ)解法二:如图建立空间直角坐标系,
则D(0,0,0),A(1,0,0),A1(1,0,
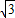 ),
),B(0,
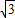 ,0),B1(0,
,0),B1(0,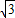 ,
,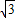 ),
),∴
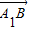 =(-1,
=(-1,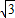 ,-
,-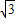 ),
),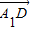 =(-1,0,-
=(-1,0,-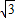 ),
),设平面A1BD的法向量为
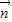 =(x,y,z),
=(x,y,z),则
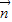
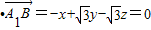
 ,
,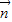
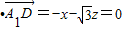
则有
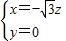 ,令z=1,得
,令z=1,得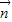 =(
=(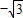 ,0,1)
,0,1)由题意,知
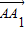 =(0,0,
=(0,0,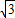 )是平面ABD的一个法向量.
)是平面ABD的一个法向量.设
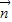 与
与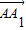 所成角为θ,
所成角为θ,则
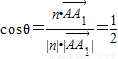 ,∴
,∴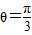 ,
,∴二面角A1-BD-A的大小是
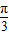 …(8分)
…(8分)(Ⅲ)解法一:由(Ⅱ)知BD⊥AC、BD⊥A1D,
设点A到平面A1BD的距离为d,
∴
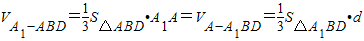 ,
,故
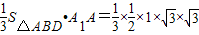
=
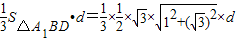
解得:
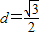 ,
,即点A到平面A1BD的距离为
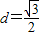 .…(12分)
.…(12分)(Ⅲ)解法二:由(Ⅱ)已知,
得
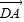 =(1,0,0),
=(1,0,0),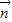 =(
=(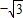 ,0,1)
,0,1)则
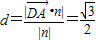
即点A到平面A1BD的距离为
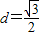 .…(12分)
.…(12分)点评:本题考查直线与平面平行、二面角、点到平面的距离的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是

 ,D是AC的中点.
,D是AC的中点.