题目内容
已知A、B、C是直线l上的不同的三点,O是直线外一点,向量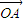 、
、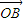 、
、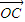 满足
满足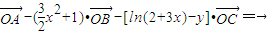 ,记y=f(x).
,记y=f(x).(1)求函数y=f(x)的解析式;
(2)若
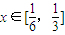 ,
,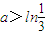 ,证明:不等式|a-lnx|>ln[f′(x)-3x]成立;
,证明:不等式|a-lnx|>ln[f′(x)-3x]成立;(3)若关于x的方程f(x)=2x+b在[0,1]上恰有两个不同的实根,求实数b的取值范围.
【答案】分析:(1)先根据 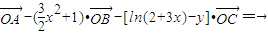 表示出向量
表示出向量  ,再由A,B,C三点共线可得到关系式
,再由A,B,C三点共线可得到关系式  ,整理即可得到答案.
,整理即可得到答案.
(2)由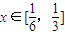 ,
,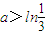 ,可知a>lnx,由(1)得
,可知a>lnx,由(1)得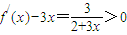 ,所以要证原不等式成立,只须证:
,所以要证原不等式成立,只须证: ,构造函数,利用函数在
,构造函数,利用函数在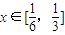 上均单调递增,则求出函数的最大值即可证得.
上均单调递增,则求出函数的最大值即可证得.
(3)将函数f(x)的解析式代入f(x)=2x+b中,整理可得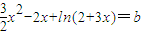 ,然后令
,然后令 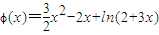 ,根据导数判断其单调性并求出其单调区间,即可求得函数φ(x)的最小值,再根据在[0,1]上恰有两个不同的实根结合函数的性质求出答案.
,根据导数判断其单调性并求出其单调区间,即可求得函数φ(x)的最小值,再根据在[0,1]上恰有两个不同的实根结合函数的性质求出答案.
解答:解:(1)由题意,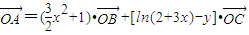
∵A、B、C三点共线,
∴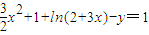
∴
(2)∵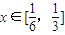 ,
,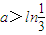 ,则a>lnx
,则a>lnx
又由(1)得,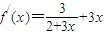 ,
,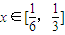 ,则
,则
∴要证原不等式成立,只须证: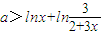 (*)
(*)
设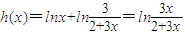 .
.
∵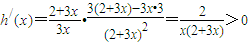
∴h(x)在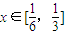 上均单调递增,则h(x)有最大值
上均单调递增,则h(x)有最大值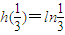 ,
,
又因为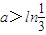 ,所以a>h(x)在
,所以a>h(x)在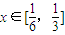 恒成立.
恒成立.
∴不等式(*)成立,即原不等式成立.
(3)方程f(x)=2x+b即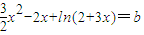 ,令
,令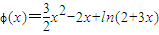 ,
,
∴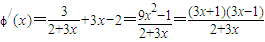
当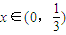 时,ϕ′(x)<0,ϕ(x)单调递减,
时,ϕ′(x)<0,ϕ(x)单调递减,
当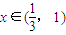 时,ϕ′(x)>0,ϕ(x)单调递增,
时,ϕ′(x)>0,ϕ(x)单调递增,
∴ϕ(x)有极小值为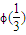 =
=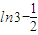 即在[0,1]上的最小值.
即在[0,1]上的最小值.
又ϕ(0)=ln2,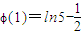 ,又
,又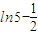 -ln2=
-ln2=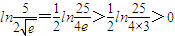
∴ln5- >ln2.
>ln2.
∴要使原方程在[0,1]上恰有两个不同实根,必须使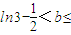 ln2.
ln2.
点评:本题以向量为依托,考查向量在几何中的应用以及利用导函数研究原函数的单调性,解题的关键是利用 A、B、C共线时,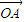 =λ
=λ 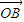 +(1-λ)
+(1-λ)  ,建立等式,同时证明不等式时利用了分离参数法,也是我们应该掌握的方法.
,建立等式,同时证明不等式时利用了分离参数法,也是我们应该掌握的方法.
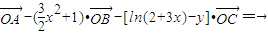 表示出向量
表示出向量 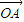 ,再由A,B,C三点共线可得到关系式
,再由A,B,C三点共线可得到关系式  ,整理即可得到答案.
,整理即可得到答案.(2)由
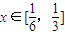 ,
,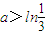 ,可知a>lnx,由(1)得
,可知a>lnx,由(1)得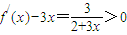 ,所以要证原不等式成立,只须证:
,所以要证原不等式成立,只须证: ,构造函数,利用函数在
,构造函数,利用函数在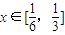 上均单调递增,则求出函数的最大值即可证得.
上均单调递增,则求出函数的最大值即可证得.(3)将函数f(x)的解析式代入f(x)=2x+b中,整理可得
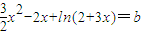 ,然后令
,然后令 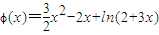 ,根据导数判断其单调性并求出其单调区间,即可求得函数φ(x)的最小值,再根据在[0,1]上恰有两个不同的实根结合函数的性质求出答案.
,根据导数判断其单调性并求出其单调区间,即可求得函数φ(x)的最小值,再根据在[0,1]上恰有两个不同的实根结合函数的性质求出答案.解答:解:(1)由题意,
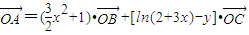
∵A、B、C三点共线,
∴
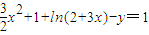
∴

(2)∵
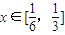 ,
,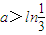 ,则a>lnx
,则a>lnx又由(1)得,
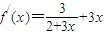 ,
,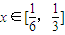 ,则
,则
∴要证原不等式成立,只须证:
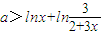 (*)
(*)设
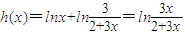 .
.∵
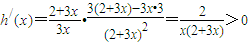
∴h(x)在
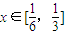 上均单调递增,则h(x)有最大值
上均单调递增,则h(x)有最大值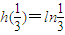 ,
,又因为
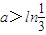 ,所以a>h(x)在
,所以a>h(x)在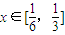 恒成立.
恒成立.∴不等式(*)成立,即原不等式成立.
(3)方程f(x)=2x+b即
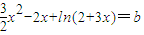 ,令
,令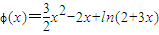 ,
,∴
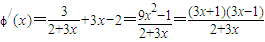
当
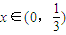 时,ϕ′(x)<0,ϕ(x)单调递减,
时,ϕ′(x)<0,ϕ(x)单调递减,当
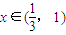 时,ϕ′(x)>0,ϕ(x)单调递增,
时,ϕ′(x)>0,ϕ(x)单调递增,∴ϕ(x)有极小值为
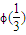 =
=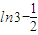 即在[0,1]上的最小值.
即在[0,1]上的最小值.又ϕ(0)=ln2,
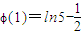 ,又
,又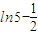 -ln2=
-ln2=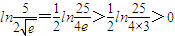
∴ln5-
 >ln2.
>ln2.∴要使原方程在[0,1]上恰有两个不同实根,必须使
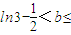 ln2.
ln2.点评:本题以向量为依托,考查向量在几何中的应用以及利用导函数研究原函数的单调性,解题的关键是利用 A、B、C共线时,
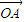 =λ
=λ 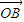 +(1-λ)
+(1-λ)  ,建立等式,同时证明不等式时利用了分离参数法,也是我们应该掌握的方法.
,建立等式,同时证明不等式时利用了分离参数法,也是我们应该掌握的方法. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目