题目内容
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
AD=a,G是EF的中点,
(1)求证:AG⊥平面BGC;
(2)求二面角B-AC-G的正弦值.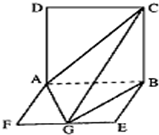
| 1 |
| 2 |
(1)求证:AG⊥平面BGC;
(2)求二面角B-AC-G的正弦值.

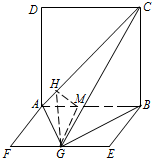
(1)证明:∵G是矩形ABEF的边EF的中点
∴AG=BG=
| 4+4 |
| 2 |
∴AG2+BG2=AB2
∴AG⊥BG
又∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
且BC⊥AB
∴BC⊥平面ABEF,
又∵AG?平面ABEF,
∴BC⊥AG
∵BC∩BG=B
∴AG⊥平面BGC;
(2)作GM⊥AB于M,则M为AB中点,M为G的射影
作GH⊥AC于H,连接MH,则所求角∠GHM
∵GM=a,MH=
| 1 |
| 2 |
| 2 |
∴GH=
| 3 |
∴sin∠GHM=
| GM |
| GH |
| ||
| 3 |

练习册系列答案
相关题目
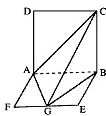 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.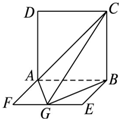 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=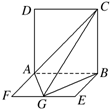 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=