题目内容
已知函数![]()
![]()
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)若函数![]() 在
在![]() 为增函数,求
为增函数,求![]() 的取值范围;
的取值范围;
(3)讨论方程![]() 解的个数,并说明理由。
解的个数,并说明理由。
(1)![]()
![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,方程无解;当
时,方程无解;当![]() 时,方程有惟一解; 当
时,方程有惟一解; 当![]() 时方程有两解。
时方程有两解。
解析:
(1)因为:![]()
![]() ,又
,又![]() 在
在![]() 处的切线方程为
处的切线方程为
![]()
所以 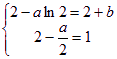 解得:
解得:![]()
![]()
(2)若函数![]() 在
在![]() 上恒成立。则
上恒成立。则![]() 在
在![]() 上恒成立,
上恒成立,
即:![]() 在
在![]() 上恒成立。所以有
上恒成立。所以有 ![]()
(3)当![]() 时,
时,![]() 在定义域
在定义域![]() 上恒大于
上恒大于![]() ,此时方程无解;
,此时方程无解;
当![]() 时,
时,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在定义域
在定义域![]() 上为增函数。
上为增函数。
![]() ,
,![]() ,所以方程有惟一解。
,所以方程有惟一解。
当![]() 时,
时,![]()
因为当![]() 时,
时,![]() ,
,![]() 在
在![]() 内为减函数;
内为减函数;
当![]() 时,
时,![]() 在
在![]() 内为增函数。
内为增函数。
所以当![]() 时,有极小值即为最小值
时,有极小值即为最小值![]() 。
。
当![]() 时,
时,![]() ,此方程无解;
,此方程无解;
当![]() 时,
时,![]() 此方程有惟一解
此方程有惟一解![]() 。
。
当![]() 时,
时,![]()
因为![]() 且
且![]() ,所以方程
,所以方程![]() 在区间
在区间![]() 上有惟一解,
上有惟一解,
因为当![]() 时,
时,![]() ,所以
,所以 ![]()
所以 ![]()
因为 ![]() ,所以
,所以 ![]()
所以 方程![]() 在区间
在区间![]() 上有惟一解。
上有惟一解。
所以方程![]() 在区间
在区间![]() 上有惟两解。
上有惟两解。
综上所述:当![]() 时,方程无解;当
时,方程无解;当![]() 时,方程有惟一解;
时,方程有惟一解;
当![]() 时方程有两解。
时方程有两解。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
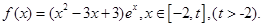
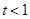 时,求函数
时,求函数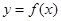 的单调区间;
的单调区间;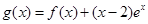 ,试问函数
,试问函数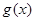 在
在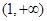 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.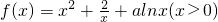 ,
,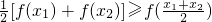 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.