题目内容
7.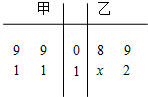 如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.(1)求x的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
分析 (1)根据两组数据的平均数相等,可得x的值,进而求出两组数据的方差,比较可得哪组学生成绩更稳定;
(2)分别计算在甲、乙两组中各抽出一名同学及成绩和低于20分的取法种数,代入古典概型概率公式,可得答案.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{4}$(9+9+11+11)=10,
$\overline{{x}_{乙}}$=$\frac{1}{4}$(8+9+10+x+12)=10,
解得:x=1 …(2分),
又${S}_{甲}^{2}$=$\frac{1}{4}$[(9-10)2+(9-10)2+(11-10)2+(11-10)2]=1;
${S}_{乙}^{2}$=$\frac{1}{4}$[(8-10)2+(9-10)2+(11-10)2+(12-10)2]=$\frac{5}{2}$,…(4分)
∴${S}_{甲}^{2}$<${S}_{乙}^{2}$,
∴甲组成绩比乙组稳定. …(6分)
(2)记甲组4名同学为:A1,A2,A3,A4;乙组4名同学为:B1,B2,B3,B4;
分别从甲乙两组中各抽取一名同学所有可能的结果为:
(A1,B1),(A1,B2),(A1,B3),(A1,B4)
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A3,B2),(A3,B3),(A3,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),共16个基本事件,
其中得分之和低于(20分)的共6个基本事件,…(10分)
∴得分之和低于(20分)的概率是:P=$\frac{6}{16}$=$\frac{3}{8}$.…(12分)
点评 本题考查了古典概型概率计算公式,茎叶图,掌握古典概型概率公式:概率=所求情况数与总情况数之比是解题的关键.

| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | -$\frac{11}{3}$ | B. | -17 | C. | 12 | D. | 13 |
| A. | $\frac{1}{4}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$+$\sqrt{2}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |