题目内容
15.定义行列式运算 |a1a2a3a4||a1a2a3a4|=a1a4-a2a3.将函数f(x)=|√3sinx1cosx||√3sinx1cosx|的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为 ( )| A. | π6π6 | B. | 5π65π6 | C. | π3π3 | D. | 2π32π3 |
分析 由条件根据函数y=Acos(ωx+φ)的图象变换规律,余弦函数的图象的对称性,可得n+π6π6=kπ,k∈z,从而求得n的最小值.
解答 解:函数f(x)=|√3sinx1cosx||√3sinx1cosx|=√3√3cosx-sinx=2cos(x+π6π6)的图象向左平移n(n>0)个单位,
所得图象对应的函数为y=2cos(x+n+π6π6),根据所得函数为偶函数,可得n+π6π6=kπ,k∈z,
则n的最小值为5π65π6,
故选:B.
点评 本题主要考查函数y=Acos(ωx+φ)的图象变换规律,余弦函数的图象的对称性,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7.过抛物线:y2=2px(p>0)的焦点F作倾斜角为60°的直线l,若直线l与抛物线在第一象限的交点为A,并且点A也在双曲线:x2a2x2a2-y2b2y2b2=1(a>0,b>0)的一条渐近线上,则双曲线的离心率为( )
| A. | √213√213 | B. | √13√13 | C. | 2√332√33 | D. | √5√5 |
3.设双曲线x2a2x2a2-y2b2y2b2=1(a>0,b>0)的一个焦点到一条渐近线的距离为a,则双曲线的离心率等于( )
| A. | √22√22 | B. | 2 | C. | √3√3 | D. | √2√2 |
20.阅读如图的程序框图,若输出的y=1212,则输入的x的值可能为( )


| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
3.已知三棱锥V-ABC,VA⊥平面ABC,在三角形ABC中,∠BAC=120°,AB=AC=VA=2,三棱锥V-ABC的外接球的表面积为( )
| A. | 16π | B. | 32π332π3 | C. | 20√5π320√5π3 | D. | 20π |
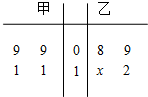 如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.