题目内容
 (2008•成都三模)如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ一点,A∈β,AC=2,∠ACP=30°,则点A到平面α的距离为( )
(2008•成都三模)如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ一点,A∈β,AC=2,∠ACP=30°,则点A到平面α的距离为( )分析:过A作AO⊥α于O,点A到平面α的距离为AO;作AD⊥PQ于D,连接OD,说明∠ADO就是二面角α-PQ-β的大小为60°.
通过三角形ADC与三角形AOD求出AO的值,即可.
通过三角形ADC与三角形AOD求出AO的值,即可.
解答: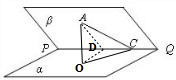 解:过A作AO⊥α于O,点A到平面α的距离为AO;
解:过A作AO⊥α于O,点A到平面α的距离为AO;
作AD⊥PQ于D,连接OD,
则AD⊥CD,AO⊥OD,∠ADO就是二面角α-PQ-β的大小为60°.
∵AC=2,∠ACP=30°,
所以AD=ACsin30°=2×
=1.
在Rt△AOD中,
=sin60°,
AO=ADsin60°=1×
=
.
故答案为:
.
 解:过A作AO⊥α于O,点A到平面α的距离为AO;
解:过A作AO⊥α于O,点A到平面α的距离为AO;作AD⊥PQ于D,连接OD,
则AD⊥CD,AO⊥OD,∠ADO就是二面角α-PQ-β的大小为60°.
∵AC=2,∠ACP=30°,
所以AD=ACsin30°=2×
| 1 |
| 2 |
在Rt△AOD中,
| AO |
| AD |
AO=ADsin60°=1×
| ||
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查空间几何体中点、线、面的关系,正确作出所求距离是解题的关键,考查计算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目