Question

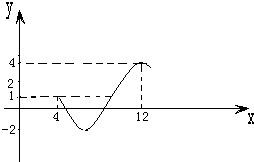如图为函数y=Asin（ωx+φ）+c（A＞0，ω＞0，φ＞0）图象的一部分．
（1）求此函数的周期及最大值和最小值；
（2）求与这个函数图象关于直线x=2对称的函数解析式．

Answer 1

分析：（1）由图象的最大值4，最小值-2，从而可得A，c，由图象可知求 T，由周期公式 T=

2π

ω

可求ω，再把f（x）的图象有一个最高点（12，4）代入可求φ，从而可求函数的解析式，
（2）设所求函数的图象上任一点（x，y）关于直线x=2的对称点为（x'，y'），则有x'=4-x，y'=y代入y=3cos

π

6

x+1中求函数y=3cos

π

6

x+1的图象关于直线x=2对称的函数解析式．

解答：解：（1）由图可知，从4～12的图象是函数y=Asin（ωx+φ）+c（A＞0，ω＞0，φ＞0）的

3

4

个周期的图象，所以A=

1

2

(4+2)=3
c=

1

2

(4-2)=1，
故函数的最大值为4，最小值为-2（4分）
∵

3T

4

=12-4=8
T=

32

3

∴ω=

3

16

π，y=3sin（

3π

16

x+φ）+1
把x=12，y=4代入上式，得φ=

π

4

所以，函数的解析式为：y=3sin（

3π

16

x+

π

4

）+1（8分）
（2）设所求函数的图象上任一点（x，y）关于直线x=2的对称点为（x'，y'），
则x'=4-x，y'=y代入y=3sin（

3π

16

x+

π

4

）+1中得y=3sin

3π

16

x+1
∴与函数y=3sin（

3π

16

x+

π

4

）+1的图象关于直线x=2对称的函数解析式为：y=3sin

3π

16

x+1（14分）

点评：本题主要考查了利用函数的部分图象求解函数的解析式，一般步骤：由函数的最值求 A，由函数的周期求ω，由函数所过的点（一般用最值点）求φ，从而可求函数的解析式；考查了由三角函数的图象关于直线对称的函数的解析式的求解．