题目内容
 如图为函数y=Asin(ωx+φ)的一段图象.
如图为函数y=Asin(ωx+φ)的一段图象.(1)请写出这个函数的一个解析式;
(2)求与(1)中函数图象关于直线x=2π,对称的函数图象的解析式,并作出它一个周期内的简图.
分析:(I)由函数的周期求出ω,由顶点的纵坐标求A,把定点的坐标代入求出φ的值,从而得到函数的解析式.
(II)设(x,y)为所求函数图象上任意一点,该点关于直线x=2π对称点为(4π-x,y),则点(4π-x,y)必在函数y=3sin(
x-
)的图象上.由此求出关于直线x=2π对称的函数图象的解析式,列表做出图象.
(II)设(x,y)为所求函数图象上任意一点,该点关于直线x=2π对称点为(4π-x,y),则点(4π-x,y)必在函数y=3sin(
| 1 |
| 2 |
| π |
| 6 |
解答:解:(I)T=
-
=4π,∵ω=
=
,又A=3,
由y=3sin(
x+φ)的图象过(
,0),∴0=3sin(
×
+φ),φ=-
(为其中一个值).
∴y=3sin(
x-
)为所求.
(II)设(x,y)为所求函数图象上任意一点,该点关于直线x=2π对称点为(4π-x,y),
则点(4π-x,y)必在函数y=3sin(
x-
)的图象上.
∴y=3sin[
(4π-x)-
],即y=-3sin(
x-
),
∴与y=3sin(
x-
)的图象关于直线x=2π对称的函数图象的解析式是y=-3sin(
x+
).
列表:
作图: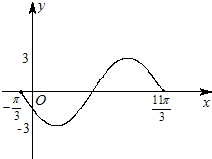
| 13π |
| 3 |
| π |
| 3 |
| 2π |
| T |
| 1 |
| 2 |
由y=3sin(
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴y=3sin(
| 1 |
| 2 |
| π |
| 6 |
(II)设(x,y)为所求函数图象上任意一点,该点关于直线x=2π对称点为(4π-x,y),
则点(4π-x,y)必在函数y=3sin(
| 1 |
| 2 |
| π |
| 6 |
∴y=3sin[
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
∴与y=3sin(
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
列表:
| x | -
|
|
|
|
| ||||||||||
|
0 |
|
π |
|
2π | ||||||||||
| y | 0 | -3 | 0 | 3 | 0 |

点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,正弦函数的对称性,属于中档题.

练习册系列答案
相关题目
 如图为函数y=Asin(ωx+φ)+c(A>0,ω>0,0<φ<2π)图象的一部分,
如图为函数y=Asin(ωx+φ)+c(A>0,ω>0,0<φ<2π)图象的一部分,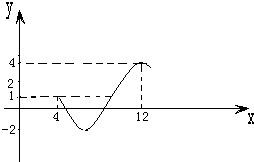 如图为函数y=Asin(ωx+φ)+c(A>0,ω>0,φ>0)图象的一部分.
如图为函数y=Asin(ωx+φ)+c(A>0,ω>0,φ>0)图象的一部分. 如图为函数
如图为函数 如图为函数y=Asin(ωx+?)+c(A>0,ω>0,?>0)图象的一部分.
如图为函数y=Asin(ωx+?)+c(A>0,ω>0,?>0)图象的一部分.