Question

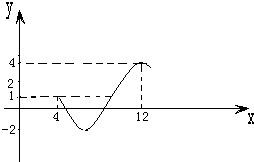
如图为函数y=Asin（ωx+φ）+c（A＞0，ω＞0，0＜φ＜2π）图象的一部分，
（1）求函数的解析式；
（2） 此函数的图象可由函数y=sinx的图象经过怎样的变换而得？

Answer 1

分析：（1）根据函数图象可知函数的振幅求得A，根据函数的最大值求得相位φ，根据最大值和最小值的距离求得函数的最小正周期进而求得ω，最后把（12，4）点代入求得∅，则函数解析式可得．
（2）根据函数图象平移法则，）先将函数的图象向左平移

π

4

个单位，然后横坐标不变，纵坐标变为原来的3倍，再纵坐标不变，横坐标变为原来的

16

3π

倍，最后向上平移1个单位，答案可得．

解答：解：（1）A=

4-(-2)

2

=3，c=

4+(-2)

2

=1
∵

3

4

T=8∴T=

32

3

即

2π

?

=

32

3

，?=

3π

16

∴y=3sin(

3π

16

x+?)+1
∵（12，4）在函数图象上
∴4=3sin(

3π

16

•12+?)+1，
即sin(

9π

4

+?)=1
∴

9π

4

+?=

π

2

+2kπ，k∈Z，得?=-

7π

4

+2kπ，k∈Z
∴函数解析式为y=3sin(

3π

16

x+

π

4

)+1
（2）先将函数的图象向左平移

π

4

个单位，
然后横坐标不变，纵坐标变为原来的3倍，
再纵坐标不变，横坐标变为原来的

16

3π

倍，
最后向上平移1个单位．

点评：本题主要考查了三角函数图象的变换．考查了学生对三角函数知识的综合理解．