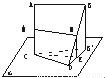
题目内容
如图,两条线段AB、CD所在的直线是异面直线,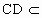 平面a
,AB∥a
,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.
平面a
,AB∥a
,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.
(1)求证:MN∥a ;
(2)若AB=CD=a,AC=b,BD=c.求线段MN的长.
答案:略
解析:
解析:
|
(1) 证明 过AC、AB作平面b 交a 于CG.∵AB∥a ,∴AB∥CG.又 AC⊥AB,∴AC⊥CG,∵AC⊥CD,∴AC⊥a .取 CE=AB=a,则四边形ACEB为矩形.∴ BE⊥a 取DE中点F,则NF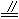 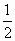 BE BE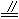 MC,∴MN MC,∴MN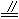 CF. CF.
∵ 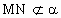 , ,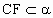 ,∴MN∥a ,∴MN∥a
(2) 解 ∵CE=AB=a,CD=a, , ,
∴ 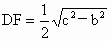 . .
∴ 或解:连 BM,DM,则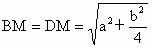 , ,
∴  . . |

练习册系列答案
相关题目
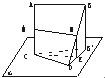 如图,两条线段AB、CD所在的直线是异面直线,CD?平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.
如图,两条线段AB、CD所在的直线是异面直线,CD?平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.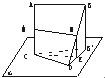 如图,两条线段AB、CD所在的直线是异面直线,CD?平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.
如图,两条线段AB、CD所在的直线是异面直线,CD?平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.