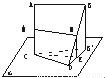
题目内容
如图,两条线段AB、CD所在的直线是异面直线,CD(1)求证:MN∥α;
(2)若AB=CD=a,AC=b,BD=c,求线段MN的长.

(1)证明:过B作BB′⊥α,垂足为B′,连结CB′、DB′,设E为B′D的中点,
连结NE、CE,则NE∥BB′且NE=![]() BB′,又AC=BB′,
BB′,又AC=BB′,
∴MC![]() NE,
NE,
即四边形MCEN为平行四边形(矩形).
∴MN∥CE.
又CE![]() α,MN
α,MN![]() α,
α,
∴MN∥α.
(2)解:由(1)知MN=CE,AB=CB′=a=CD,B′D=![]() =
=![]() ,
,
∴CE=![]() =
=![]() ,
,
即线段MN的长为![]() .
.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
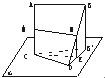 如图,两条线段AB、CD所在的直线是异面直线,CD?平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.
如图,两条线段AB、CD所在的直线是异面直线,CD?平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.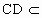 平面a
,AB∥a
,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.
平面a
,AB∥a
,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.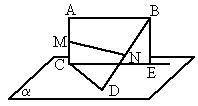
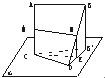 如图,两条线段AB、CD所在的直线是异面直线,CD?平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.
如图,两条线段AB、CD所在的直线是异面直线,CD?平面α,AB∥α,M、N分别是AC、BD的中点,且AC是AB、CD的公垂线段.