题目内容
已知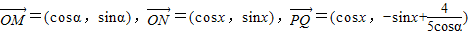
(1)当
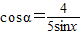 时,求函数
时,求函数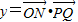 的最小正周期;
的最小正周期;(2)当
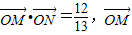 ∥
∥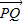 ,α-x,α+x都是锐角时,求cos2α的值.
,α-x,α+x都是锐角时,求cos2α的值.
【答案】分析:(1)根据函数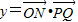 ,
,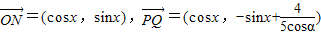 ,我们可给出函数的解析式,根据三角恒等变换,我们可将函数的解析式化为余弦型函数的形式,进而根据T=
,我们可给出函数的解析式,根据三角恒等变换,我们可将函数的解析式化为余弦型函数的形式,进而根据T=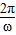 ,求出函数的最小正周期.
,求出函数的最小正周期.
(2)因为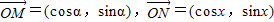 ,我们易结合
,我们易结合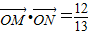 ,再根据α-x、α+x是锐角,我们易求出α-x、α+x的三角函数值,再根据2α=(α-x)+(α+x),求出cos2α的值.
,再根据α-x、α+x是锐角,我们易求出α-x、α+x的三角函数值,再根据2α=(α-x)+(α+x),求出cos2α的值.
解答:解:(1)∵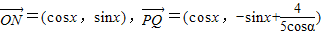 ,
,
所以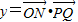 =
=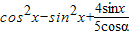 .
.
又∵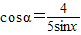 ,
,
∴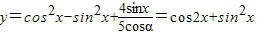
=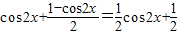 .
.
所以该函数的最小正周期是π.
(2)因为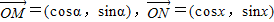
所以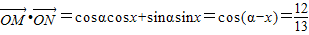
∵α-x是锐角
∴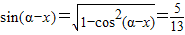
∵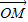 ∥
∥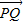
∴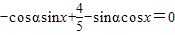 ,即
,即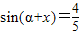
∵α+x是锐角
∴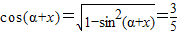
∴cos2α=cos[(α+x)+(α-x)]=cos(α+x)cos(α-x)-sin(α+x)sin(α-x)
=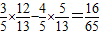 ,即cos2α=
,即cos2α=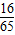 .
.
点评:本题考查的知识点是平面向量的数量积运算,三角函数恒等变换,平行(共线)向量,两角和的余弦公式,解答的关键(1)中要将函数的解析式化为余弦型函数的形式,(2)中关键是分析已知角与未知角的关系.
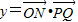 ,
,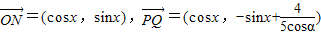 ,我们可给出函数的解析式,根据三角恒等变换,我们可将函数的解析式化为余弦型函数的形式,进而根据T=
,我们可给出函数的解析式,根据三角恒等变换,我们可将函数的解析式化为余弦型函数的形式,进而根据T=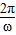 ,求出函数的最小正周期.
,求出函数的最小正周期.(2)因为
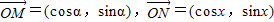 ,我们易结合
,我们易结合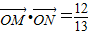 ,再根据α-x、α+x是锐角,我们易求出α-x、α+x的三角函数值,再根据2α=(α-x)+(α+x),求出cos2α的值.
,再根据α-x、α+x是锐角,我们易求出α-x、α+x的三角函数值,再根据2α=(α-x)+(α+x),求出cos2α的值.解答:解:(1)∵
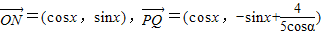 ,
,所以
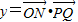 =
=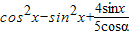 .
.又∵
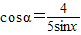 ,
,∴
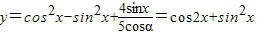
=
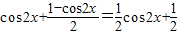 .
.所以该函数的最小正周期是π.
(2)因为
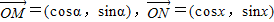
所以
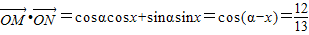
∵α-x是锐角
∴
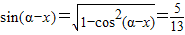
∵
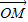 ∥
∥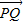
∴
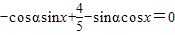 ,即
,即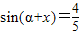
∵α+x是锐角
∴
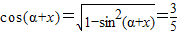
∴cos2α=cos[(α+x)+(α-x)]=cos(α+x)cos(α-x)-sin(α+x)sin(α-x)
=
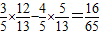 ,即cos2α=
,即cos2α=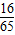 .
.点评:本题考查的知识点是平面向量的数量积运算,三角函数恒等变换,平行(共线)向量,两角和的余弦公式,解答的关键(1)中要将函数的解析式化为余弦型函数的形式,(2)中关键是分析已知角与未知角的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
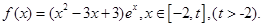
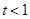 时,求函数
时,求函数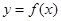 的单调区间;
的单调区间;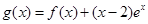 ,试问函数
,试问函数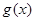 在
在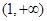 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.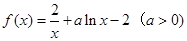 .
.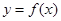 在点
在点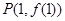 处的切线与直线
处的切线与直线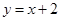 垂直,求函数
垂直,求函数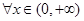 都有
都有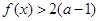 成立,试求
成立,试求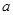 的取值范围;
的取值范围;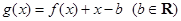 .当
.当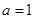 时,函数
时,函数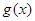 在区间
在区间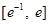 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围. ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。