题目内容
(本题满分14分)定义在D上的函数 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数 的上界。
的上界。
已知函数 ,
,
(1)当 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围;
(3)若 ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。
【答案】
解:(1)当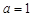 时,
时,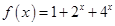 .
.
∵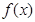 在
在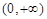 上递增,所以
上递增,所以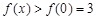 ,
,
即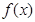 在
在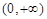 上的值域为
上的值域为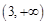 . …………………………………2分
. …………………………………2分
故不存在常数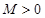 ,使
,使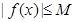 成立.
成立.
所以函数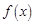 在
在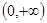 上不是有界函数. ……………………………………4分
上不是有界函数. ……………………………………4分
(2)∵函数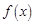 在
在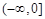 上是以3为上界的有界函数,
上是以3为上界的有界函数,
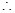
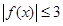 在
在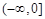 上恒成立.
上恒成立. 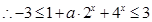 ,
,
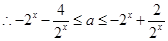 在
在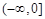 上恒成立.
上恒成立.
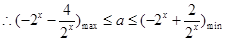 ……………………………6分
……………………………6分
设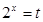 ,
,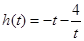 ,
,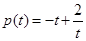 .
.
由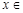
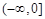 ,得
,得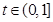 .设
.设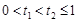 ,则
,则
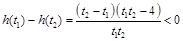 ,
,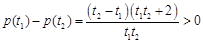 ,
,
所以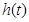 在
在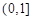 上递增,
上递增,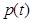 在
在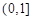 上递减.
上递减.
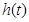 在
在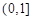 上的最大值为
上的最大值为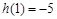 ,
,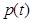 在
在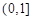 上的最小值为
上的最小值为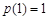 .
.
所以实数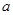 的取值范围为
的取值范围为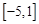 . …………………………………………… 9分
. …………………………………………… 9分
(3))方法一: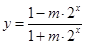 ,
,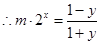 .
.
∵ m>0 , ,
,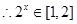 .
.
∴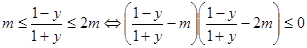
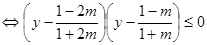 ,
,
∵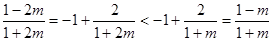
∴ .
…………………………………………11分
.
…………………………………………11分
① 当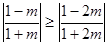 ,即
,即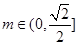 时,
时,
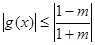 ,此时
,此时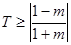 ;
;
② 当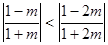 ,即
,即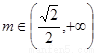 时,
时,
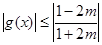 ,此时
,此时 .
.
综上所述,当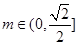 时,
时,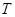 的取值范围是
的取值范围是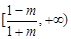 ;当
;当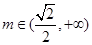 时,
时,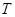 的取值范围是
的取值范围是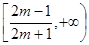 ………………………………………………………14分
………………………………………………………14分
方法二: 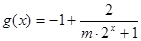 .
.
令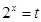 ,因为
,因为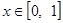 ,所以
,所以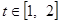 .
.
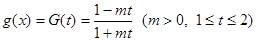 .
.
因为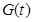 在
在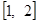 上是减函数,所以
上是减函数,所以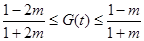 .…………………11分
.…………………11分
又因为函数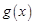 在
在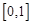 上的上界是
上的上界是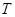 ,所以
,所以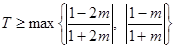 .
.
当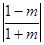

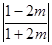 时,
时,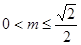 ,
,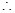
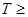
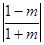
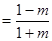 ;
;
当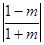
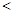
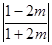 时,
时,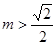 ,
,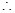
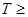
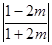
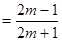 .……………………14分
.……………………14分
【解析】略

练习册系列答案
相关题目
 ,且椭圆短轴的两个端点与
,且椭圆短轴的两个端点与 构成正三角形.
构成正三角形. 与椭圆交于不同两点P、Q,若在
与椭圆交于不同两点P、Q,若在 轴上存在定点E(
轴上存在定点E( ,0),使
,0),使 恒为定值,求
恒为定值,求 ,且与定直线
,且与定直线 相切.
相切. 的方程;
的方程; 是轨迹
是轨迹 、
、 为切点作轨迹
为切点作轨迹 ,证明:
,证明: .
. 相切,点C在
相切,点C在 上.
上. 的直线与曲线交于A、B两点.问直线
的直线与曲线交于A、B两点.问直线 是以
是以 为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.
为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.