题目内容
(1991•云南)在体积为V的斜三棱柱ABC-A′B′C′中,已知S是侧棱CC′上的一点,过点S,A,B的截面截得的三棱锥的体积为V1,那么过点S,A′,B′的截面截得的三棱锥的体积为
-V1
-V1.
| V |
| 3 |
| V |
| 3 |
分析:我们可设侧棱CC′到侧面ABB′A′的距离为d,根据斜三棱柱ABC-A′B′C′的体积等于侧面ABB′A′的面积与d的乘积的一半,再根据同底同高的棱锥体积公式,求出四棱椎S-ABB′A′的体积,进而得到答案.
解答: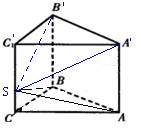 解:设侧棱CC′到侧面ABB′A′的距离为d
解:设侧棱CC′到侧面ABB′A′的距离为d
∵斜三棱柱ABC-A′B′C′的体积等于侧面ABB′A′的面积与d的乘积的一半,
∴V=
SABB'A'•d,
又四棱椎S-ABB′A′的体积等于
SABB'A'•d=
V,
则那么过点S,A′,B′的截面截得的三棱锥的体积为等于 V-V1-
V=
-V1.
故答案为:
-V1.
 解:设侧棱CC′到侧面ABB′A′的距离为d
解:设侧棱CC′到侧面ABB′A′的距离为d∵斜三棱柱ABC-A′B′C′的体积等于侧面ABB′A′的面积与d的乘积的一半,
∴V=
| 1 |
| 2 |
又四棱椎S-ABB′A′的体积等于
| 1 |
| 3 |
| 2 |
| 3 |
则那么过点S,A′,B′的截面截得的三棱锥的体积为等于 V-V1-
| 2 |
| 3 |
| V |
| 3 |
故答案为:
| V |
| 3 |
点评:本题考查的知识点是棱柱的体积,棱锥的体积,考查割补法.属于基础题.

练习册系列答案
相关题目