题目内容
11.已知函数f(x)=aex-be-x-2x(a,b∈R)的导函数f'(x)为偶函数,且曲线y=f(x)在点(0,f(0))处的切线斜率0(其中e=2.71828…)(1)求a,b的值;
(2)设g(x)=f(2x)-4mf(x),若g(x)有极值.
(i)求m的取值范围;
(ii)试比较em-1与me-1的大小并证明你的结论.
分析 (1)求导数,利用f′(x)为偶函数,f′(0)=a+b-2=0,即可求a,b的值;
(2)(i)g′(x)=2(ex+e-x-2)(ex+e-x-2m+2),由ex+e-x-2≥0,只要讨论ex+e-x-2m+2的符号,即可求m的取值范围;
(ii)由上知,m>2,比较em-1与me-1的大小,即比较m-1与(e-1)lnm的大小,即确定m-1-(e-1)lnm的符号.考查M(x)=x-(e-1)lnx-1,x>2,M′(x)=1-$\frac{e-1}{x}$$>1-\frac{e-1}{2}$>0,M(x)在(2,+∞)上单调递增且M(e)=0,分类讨论,即可比较em-1与me-1的大小并证明你的结论.
解答 解:(1)∵f(x)=aex-be-x-2x,
∴f′(x)=aex+be-x-2
∵f′(x)为偶函数,
∴f′(-x)=f′(x),
∴(a-b)(ex-e-x)=0,
∴a=b,
∵f′(0)=a+b-2=0,
∴a=b=1;
(2)(i)g(x)=f(2x)-4mf(x)=e2x-e-2x-4m(ex-e-x)+(8m-4)x,
∴g′(x)=2(ex+e-x-2)(ex+e-x-2m+2),
由ex+e-x-2≥0,只要讨论ex+e-x-2m+2的符号.
①2m-2<2,即m<2时,ex+e-x-2m+2>0,g′(x)>0,此时g(x)无极值;
②2m-2=2,即m=2时,ex+e-x-2m+2≥0,g′(x)≥0,此时g(x)无极值;
③2m-2>2,即m>2时,令t=ex,则$t+\frac{1}{t}-2m+2=0$的两个根为t1,2=m-1±$\sqrt{m(m-2)}$>0,
则g′(x)=0有两个根x1=$\frac{1}{2}$lnt1,x2=$\frac{1}{2}$lnt2,
x<x1时,g′(x)>0;x1<x<x2,g′(x)<0;x>x2,g′(x)>0;
∴x=x1时取得极大值,x=x2时取得极小值,
综上,m的取值范围为(2,+∞);
(ii)由上知,m>2,比较em-1与me-1的大小,即比较m-1与(e-1)lnm的大小,即确定m-1-(e-1)lnm的符号.
考查M(x)=x-(e-1)lnx-1,x>2,M′(x)=1-$\frac{e-1}{x}$$>1-\frac{e-1}{2}$>0
∴M(x)在(2,+∞)上单调递增且M(e)=0,
∴x=e时,M(x)=0,即x-1=(e-1)lnx,∴ex-1=xe-1;
x>e时,M(x)>0,即x-1>(e-1)lnx,∴ex-1>xe-1;
2<x<e时,M(x)<0,即x-1<(e-1)lnx,∴ex-1<xe-1.
综上,m=e时,ex-1=xe-1;m>e时,ex-1>xe-1;m<e时,ex-1<xe-1.
点评 本题考查导数知识的综合运用,考查函数的单调性与极值,考查大小比较,考查分类讨论的数学数学,有难度.

| 2 | 4 | 8 | 14 | … |
| 6 | 10 | 16 | 24 | … |
| 12 | 18 | 26 | 36 | … |
| 20 | 28 | 38 | 50 | … |
| … | … | … | … | … |
(Ⅱ) 若aij=502,求i,j的值;(只需写出结论)
(Ⅲ)设bn=ann,cn=$\frac{1}{2^n}-\frac{4}{{{b_{n+1}}-2}}$(n∈N*,),记数列{cn}的前n项和为Sn,求Sn;并求正整数k,使得对任意n∈N*,均有Sk≥Sn.
| A. | $({0,\frac{1}{10}})$ | B. | $({0,\frac{1}{10}})∪({10,+∞})$ | C. | $({\frac{1}{10},10})$ | D. | (10,+∞) |
(参考数据:P(μ-σ≤ξ≤μ+σ)=0.6286,P(μ-2σ≤ξ≤μ+2σ)=0.9544,P(μ-3σ≤ξ≤μ+σ3)=0.9974)
| A. | 0.0215 | B. | 0.1359 | C. | 0.1574 | D. | 0.2718 |
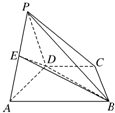 如图,在四棱锥PABCD中,底面ABCD是直角梯形,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.
如图,在四棱锥PABCD中,底面ABCD是直角梯形,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.