题目内容
球的体积是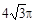
，则球的表面积是 ；
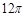
解析试题分析：设球的半径为R，则
，所以
，所以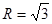球的表面积为
。
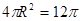考点：球的体积公式；球的表面积公式。
点评：熟记球的球的体积公式和表面积公式，属于基础题型。
练习册系列答案
相关题目
题目内容
球的体积是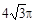，则球的表面积是 ；
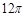
解析试题分析：设球的半径为R，则，所以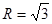，所以球的表面积为。
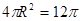考点：球的体积公式；球的表面积公式。
点评：熟记球的球的体积公式和表面积公式，属于基础题型。
，在该几何体的正视图中，这条棱的投影是长为
的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别为
和
的线段，则
的最大值为 
，腰和上底均为1（如图），则平面图形的实际面积为 ．
平面ABC，AB
BC，DA=AB=BC=
,
高为
则它最多能放入半径为
的球 个。
的中线AF与中位线DE相交于G，已知
是
绕边DE旋转过程中的一个图形，给出四个命题：
在
上的射影在线段
上；
;
的体积有最大值; 
与
不可能垂直．以上正确的命题序号是 
是棱长为
的正方体的一个顶点，过从此顶点出发的三条棱的中点作截面，对正方体的所有顶点都如此操作，所得的各截面与正方体各面共同围成一个多面体，则关于此多面体有以下结论：①有
个顶点；②有
条棱；③有
；⑤体积为
．其中正确的结论是____________．（要求填上所有正确结论的序号）
的球体完全装入底面半径是
的圆柱形桶中，则桶的最小高度是 ．