题目内容
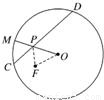
如图，一圆形纸片的圆心为O, F是圆内一定点，M是圆周
上一动点，把纸片折叠使M与F重合，然后抹平纸片，折痕
为CD, 设CD与OM交于P, 则点P的轨迹是（ 
）
| A．椭圆 | B．双曲线 |
| C．抛物线 | D．圆 |
A
解析考点：椭圆的定义．
分析：根据CD是线段MF的垂直平分线．可推断出|MP|=|PF|，进而可知|PF|+|PO|=|PM|+|PO|=|MO|结果为定值，进而根据椭圆的定义推断出点P的轨迹．
解：由题意知，CD是线段MF的垂直平分线．
∴|MP|=|PF|，
∴|PF|+|PO|=|PM|+|PO|=|MO|（定值），
又显然|MO|＞|FO|，
∴根据椭圆的定义可推断出点P轨迹是以F、O两点为焦点的椭圆．
故选A
练习册系列答案
相关题目
3、如图，一圆形纸片的圆心为O，F是圆内一定点，M是圆周上一动点，把纸片折叠使M与F重合，然后抹平纸片，折痕为CD，设CD与OM交于点P，则点P的轨迹是（ ）
如图，一圆形纸片的圆心为O，F是圆内一定点，M是圆周上一动点，MF的垂直平分线CD交OM于P，则点P的轨迹是（ ）
）