题目内容
在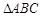 中,角
中,角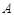 ,
,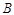 ,
,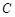 所对的边分别是
所对的边分别是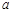 ,
,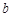 ,
,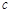 ,已知
,已知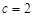 ,
,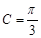 .
.
(1)若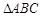 的面积等于
的面积等于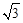 ,求
,求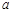 ,
,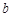 ;
;
(2)若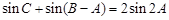 ,求
,求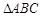 的面积.
的面积.
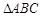 中,角
中,角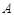 ,
,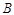 ,
,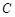 所对的边分别是
所对的边分别是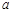 ,
,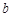 ,
,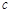 ,已知
,已知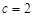 ,
,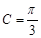 .
.(1)若
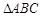 的面积等于
的面积等于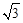 ,求
,求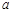 ,
,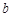 ;
;(2)若
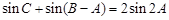 ,求
,求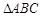 的面积.
的面积.(1)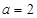 ,
,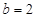 (2)
(2)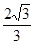
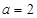 ,
,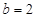 (2)
(2)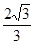
试题分析:
(1)要求两边
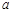 ,
,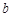 的长,需要建立两个关于它们的方程式.根据已知条件,利用余弦定理建立第一个方程;根据面积公式
的长,需要建立两个关于它们的方程式.根据已知条件,利用余弦定理建立第一个方程;根据面积公式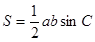 的第二个方程式.两个方程联立可得
的第二个方程式.两个方程联立可得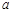 ,
,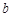 .
.(2)要求面积,根据
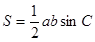 知:得求出
知:得求出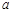 ,
,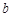 ,由于
,由于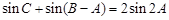 中含有
中含有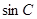 ,所以根据
,所以根据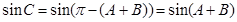 ,将
,将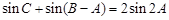 转化为关于角
转化为关于角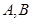 的式子,通过化简可得
的式子,通过化简可得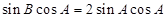 ,进而通过讨论
,进而通过讨论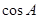 是否等于零,得出两种不同情况下
是否等于零,得出两种不同情况下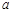 ,
,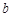 的值,从而求出面积.
的值,从而求出面积.(1)由余弦定理
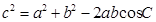 及已知条件得,
及已知条件得, ,
, 又因为
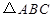 的面积等于
的面积等于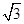 ,所以
,所以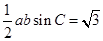 ,得
,得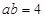 .
.联立方程组
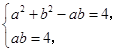 解得
解得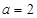 ,
,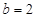 .
.(2)根据
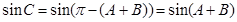 ,
,由题意得
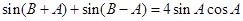 ,
,即
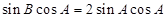 ,则在
,则在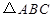 中:
中:当
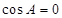 时,
时,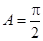 ,
,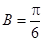 ,此时
,此时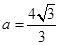 ,
, ,面积
,面积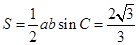 .
.当
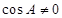 时,得
时,得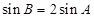 ,由正弦定理得
,由正弦定理得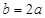 ,
, 联立方程组
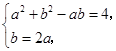 解得
解得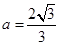 ,
,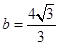 ,面积
,面积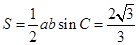 .
.综上可知:
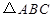 的面积
的面积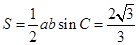 .
.
练习册系列答案
相关题目
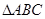 三个内角
三个内角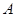 ,
,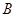 ,
,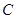 的对边分别为
的对边分别为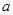 ,
,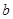 ,
,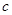 ,且
,且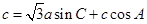 ,
,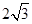 ,
,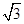 ,求
,求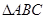 中,
中,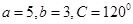 ,则
,则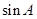 的值为( )
的值为( )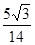
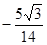
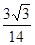
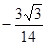
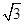 ,则角A等于( ).
,则角A等于( ).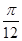
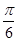
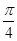
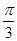
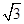 )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
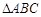 中,
中,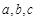 为角
为角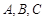 所对的边,且
所对的边,且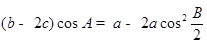 .
.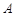 的值;
的值;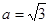 ,则求
,则求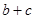 的取值范围.
的取值范围.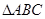 中,
中,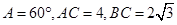 ,则
,则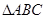 中,
中,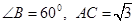 ,则
,则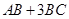 的最大值为 .
的最大值为 .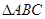 为锐角三角形,
为锐角三角形,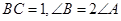 ,则
,则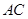 的取值范围为_______.
的取值范围为_______.