题目内容
9.若在区间(0,m]上恰有一个实数a使函数f(x)=x4-ax2-1有整数零点,则实数m的取值范围是[$\frac{15}{4}$,$\frac{80}{9}$).分析 化简可得a=$\frac{{x}^{4}-1}{{x}^{2}}$=x2-$\frac{1}{{x}^{2}}$,从而可判断其在(-∞,0)上是减函数,在(0,+∞)上是增函数;从而求实数m的取值范围.
解答 解:令f(x)=x4-ax2-1=0得,
a=$\frac{{x}^{4}-1}{{x}^{2}}$=x2-$\frac{1}{{x}^{2}}$;
易知a=x2-$\frac{1}{{x}^{2}}$在(-∞,0)上是减函数,在(0,+∞)上是增函数;
且当x2=1时,a=0,当x2=4时,a=$\frac{15}{4}$,当x2=9时,a=$\frac{80}{9}$;
又∵在区间(0,m]上恰有一个实数a,使函数f(x)=x4-ax2-1有整数零点,
∴实数m的取值范围是[$\frac{15}{4}$,$\frac{80}{9}$);
故答案为:[$\frac{15}{4}$,$\frac{80}{9}$).
点评 本题考查了函数的性质的判断与应用,属于基础题.

练习册系列答案
相关题目
20.若正方形的棱长为2$\sqrt{2}$,则以该正方形各个面的中心为顶点的凸多面体的体积为( )
| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
14.下列几何体是台体的是( )
| A. | 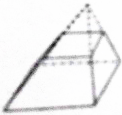 | B. | 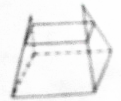 | C. |  | D. |  |
19.袋中有大小相同的红球6个,白球5个,从袋中每次任意取出1个球,直到取出的球是白球时为止,所需要的取球的次数为随机变量ξ,则ξ的可能值为( )
| A. | 1,2,…,6 | B. | 1,2,…,7 | C. | 1,2,…,11 | D. | 1,2,3… |