题目内容
已知函数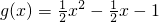 ,令
,令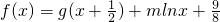 (m∈R).
(m∈R).
(1)若?x>0,,使f(x)≤0成立,求实数m的取值范围;
(2)设1<m≤e,H(x)=f(x)-(m+1)x,证明:对?x1,x2∈[1,m],恒有H(x1)-H(x2)<1.
解:(1)由题意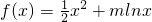 ,得
,得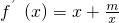 .
.
①当m>0时, ,因此f(x)在(0,+∞)上单调递增,由对数函数的性质,知f(x)的值域为R,因此?x>0,使f(x)≤0成立;
,因此f(x)在(0,+∞)上单调递增,由对数函数的性质,知f(x)的值域为R,因此?x>0,使f(x)≤0成立;
②当m=0时, ,对?x>0,f(x)>0恒成立;
,对?x>0,f(x)>0恒成立;
③当m<0时,由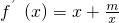 得
得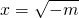 ,
,
此时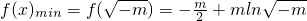 .
.
令 .
.
所以对?x>0,f(x)>0恒成立,则实数m的取值范围是(-e,0].
故?x>0,使f(x)≤0成立,实数m的取值范围是(-∞,-e]∪(0,+∞).
(2)∵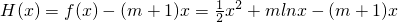 ,
,
∴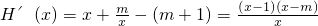 .
.
?x∈[1,m], ≤0,所以函数H(x)在[1,m]上单调递减.
≤0,所以函数H(x)在[1,m]上单调递减.
于是 .
.
 .
.
记 ,
,
则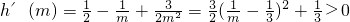 ,
,
所以函数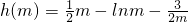 在(1,e]上是单调增函数,
在(1,e]上是单调增函数,
所以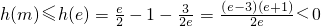 ,
,
故对?x1,x2∈[1,m],恒有H(x1)-H(x2)<1.
分析:(1)由题意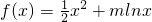 ,得
,得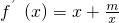 .讨论m的范围判断函数的单调性与其最值,通过最小值与0的关系得到m的范围.
.讨论m的范围判断函数的单调性与其最值,通过最小值与0的关系得到m的范围.
(2)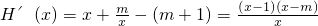 ≤0,所以函数H(x)在[1,m]上单调递减.
≤0,所以函数H(x)在[1,m]上单调递减. ,所以设
,所以设 判断其单调性求其最值即可证得.
判断其单调性求其最值即可证得.
点评:解决至少存在问题可从正面入手找到存在的原因也可以先做它的反面,证明不等式问题一般利用导数判断函数单调性通过函数的单调性求函数的最值,在利用最值求证不等式,函数与不等式结合是高考考查的热点之一.
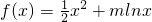 ,得
,得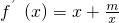 .
.①当m>0时,
 ,因此f(x)在(0,+∞)上单调递增,由对数函数的性质,知f(x)的值域为R,因此?x>0,使f(x)≤0成立;
,因此f(x)在(0,+∞)上单调递增,由对数函数的性质,知f(x)的值域为R,因此?x>0,使f(x)≤0成立;②当m=0时,
 ,对?x>0,f(x)>0恒成立;
,对?x>0,f(x)>0恒成立;③当m<0时,由
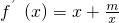 得
得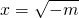 ,
,| x | 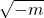 | 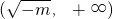 | |
| - | 0 | + | |
| f(x) | ↘ | 极小值 | ↗ |
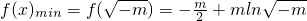 .
.令
 .
.所以对?x>0,f(x)>0恒成立,则实数m的取值范围是(-e,0].
故?x>0,使f(x)≤0成立,实数m的取值范围是(-∞,-e]∪(0,+∞).
(2)∵
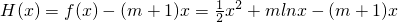 ,
,∴
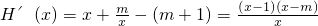 .
.?x∈[1,m],
 ≤0,所以函数H(x)在[1,m]上单调递减.
≤0,所以函数H(x)在[1,m]上单调递减.于是
 .
. .
.记
 ,
,则
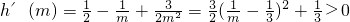 ,
,所以函数
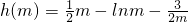 在(1,e]上是单调增函数,
在(1,e]上是单调增函数,所以
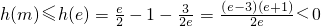 ,
,故对?x1,x2∈[1,m],恒有H(x1)-H(x2)<1.
分析:(1)由题意
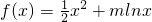 ,得
,得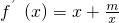 .讨论m的范围判断函数的单调性与其最值,通过最小值与0的关系得到m的范围.
.讨论m的范围判断函数的单调性与其最值,通过最小值与0的关系得到m的范围.(2)
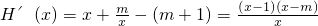 ≤0,所以函数H(x)在[1,m]上单调递减.
≤0,所以函数H(x)在[1,m]上单调递减. ,所以设
,所以设 判断其单调性求其最值即可证得.
判断其单调性求其最值即可证得.点评:解决至少存在问题可从正面入手找到存在的原因也可以先做它的反面,证明不等式问题一般利用导数判断函数单调性通过函数的单调性求函数的最值,在利用最值求证不等式,函数与不等式结合是高考考查的热点之一.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
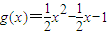 ,令
,令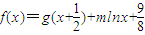 (m∈R).
(m∈R).