题目内容
要建造一个无盖长方体水池,底面一边长固定为8m,最大装水量为72m3,池底和池壁的造价分别为2a元/m2、a元/m2,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
分析:设水池底另一边长b,高h,则8bh=72,即bh=9.总造价S=2a•8b+a•2•(bh+8h)=(b+h)•16a+18a≥16a•2
+18a=114a.由此能求出水池底边和高均为3米时,水池造价最低,最低造价是114a.
| bh |
解答:解:设水池底另一边长b,高h,
则8bh=72,即bh=9,
总造价S=2a•8b+a•2•(bh+8h)
=2a•8b+2a•(9+8h)
=(b+h)•16a+18a
≥16a•2
+18a
=16a•2•3+18a
=114a.当且仅当b=h=3时,等号成立.
所以,水池底边和高均为3米时,水池造价最低,最低造价是114a.
则8bh=72,即bh=9,
总造价S=2a•8b+a•2•(bh+8h)
=2a•8b+2a•(9+8h)
=(b+h)•16a+18a
≥16a•2
| bh |
=16a•2•3+18a
=114a.当且仅当b=h=3时,等号成立.
所以,水池底边和高均为3米时,水池造价最低,最低造价是114a.
点评:本题考查解函数在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意均值定理的灵活运用.

练习册系列答案
相关题目
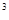 ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2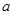 元/
元/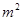 、
、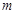 ,最大装水量为72
,最大装水量为72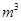 ,池底和池壁的造价分别为
,池底和池壁的造价分别为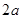 元
元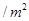 、
、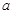 元
元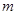 ,最大装水量为72
,最大装水量为72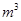 ,池底和池壁的造价分别为
,池底和池壁的造价分别为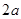 元
元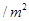 、
、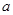 元
元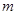 ,最大装水量为72
,最大装水量为72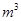 ,池底和池壁的造价分别为
,池底和池壁的造价分别为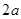 元
元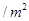 、
、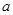 元
元