题目内容
①由“若a,b,c∈R,则(ab)c=a(bc)”类比“若a、b、c为三个向量,则(a·b)c=a(b·c)”;
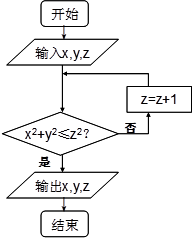
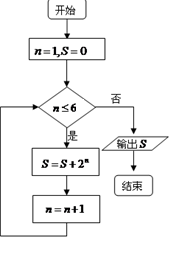
②在数列{an}中,a1=0,an+1=2an+2,猜想an=2n-2;
③在平面内“三角形的两边之和大于第三边”类比在空间中“四面体的任意三个面的面积之和大于第四个面的面积”;
上述三个推理中,正确的个数为( )
| A.0 | B.1 | C.2 | D.3 |

解析试题分析:①显然错误,向量没有结合律;
②根据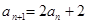 ,可构造出
,可构造出 ,即
,即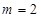 ,可得
,可得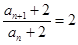 ,该数列是公比为2,首项是
,该数列是公比为2,首项是 的等比数列,所以其通项公式为
的等比数列,所以其通项公式为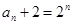 ,可得
,可得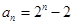 ,正确;
,正确;
③四面体就是三棱锥,可看作是底面三角形中任取一点,将其向上提而形成的几何体,显然三个侧面的面积之和大于底面面积.正确.
考点:向量运算定律;利用递推公式构造等比数列求通项公式;空间几何的猜想.类比推理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用数学归纳法证明“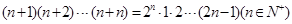 时,从“
时,从“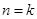 到
到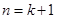 ”时,左边应增添的式子是( ).
”时,左边应增添的式子是( ).
A.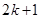 | B.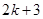 | C.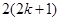 | D.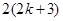 |
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
| A.假设三内角都不大于60度 |
| B.假设三内角都大于60度 |
| C.假设三内角至多有一个大于60度 |
| D.假设三内角至多有两个大于60度 |
用反证法证明命题“三角形的内角至多有一个钝角”时,假设的内容应为( )
| A.假设至少有一个钝角 | B.假设至少有两个钝角 |
| C.假设没有一个钝角 | D.假设没有一个钝角或至少有两个钝角 |
用反证法证明命题“设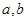 为实数,则方程
为实数,则方程 至少有一个实根”时,要做的假设是( )
至少有一个实根”时,要做的假设是( )
A.方程 没有实根 没有实根 | B.方程 至多有一个实根 至多有一个实根 |
C.方程 至多有两个实根 至多有两个实根 | D.方程 恰好有两个实根 恰好有两个实根 |
下列推理是归纳推理的是( )
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜想出椭圆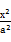 + +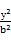 =1的面积S=πab =1的面积S=πab |
| D.以上均不正确 |