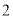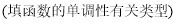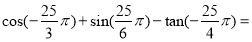题目内容
直线l经过点 ,且和圆C:
,且和圆C: 相交,截得弦长为
相交,截得弦长为 ,求l的方程.
,求l的方程.
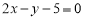 或
或
【解析】
试题分析:首先确定过点垂直于轴的直线与圆相切不合题意.设所求直线的斜率 ,写出点斜式方程,设弦心距为
,写出点斜式方程,设弦心距为 ,根据直线与圆相交时半径、半弦、弦心距的关系列方程,解出
,根据直线与圆相交时半径、半弦、弦心距的关系列方程,解出 的值即可写出所求直线的方程.
的值即可写出所求直线的方程.
试题解析:如图易知直线 的斜率
的斜率 存在,设直线
存在,设直线 的方程为
的方程为 .
.
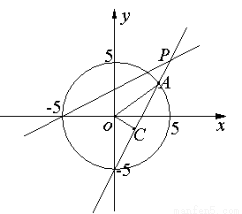
圆 :
: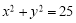 的圆心为
的圆心为 , 半径
, 半径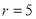 ,
,
圆心到直线l的距离 .
.
在 中,
中, ,
,
 .
. ,
,
∴ 或
或 .
.
 的方程为
的方程为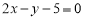 或
或 12分
12分
考点:1、直线方程;2、圆的方程;3、直线与圆的位置关系.

练习册系列答案
相关题目