题目内容
已知F1,F2分别是双曲线
-
=1(a>0,b>0)的左右焦点,P为双曲线右支上一点,且满足|PF2|=|F1F2|,若直线PF1与圆x2+y2=a2相切,则双曲线的离心率e的值为( )
| x2 |
| a2 |
| y2 |
| b2 |
分析:设PF1与圆相切于点M,利用|PF2|=|F1F2|,直线PF1与圆x2+y2=a2相切,可得几何量之间的关系,从而可求双曲线的离心率e的值.
解答:解:设PF1与圆相切于点M,则
因为|PF2|=|F1F2|,所以△PF1F2为等腰三角形
所以|F1M|=
|PF1|
又因为在直角△F1MO中,|F1M|2=|F1O|2-a2=c2-a2,所以|F1M|=b=
|PF1|①
又因为|PF1|=|PF2|+2a=2c+2a ②,c2=a2+b2 ③
由①②③得
=
故选B.
因为|PF2|=|F1F2|,所以△PF1F2为等腰三角形
所以|F1M|=
| 1 |
| 4 |
又因为在直角△F1MO中,|F1M|2=|F1O|2-a2=c2-a2,所以|F1M|=b=
| 1 |
| 4 |
又因为|PF1|=|PF2|+2a=2c+2a ②,c2=a2+b2 ③
由①②③得
| c |
| a |
| 5 |
| 3 |
故选B.
点评:本题考查直线与圆相切,考查双曲线的定义,考查双曲线的定义,属于中档题.

练习册系列答案
相关题目
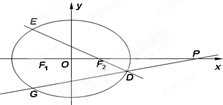 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: