题目内容
（本题满分15分）如图，设抛物线
的准线与x轴交于点
,
焦点为
为焦点，离心率为
的椭圆
与抛物线
在x轴上方的交点为P
，延长
交抛物线于点Q,M是抛物线上一动点，且M在P与Q之间运动。
1） 当m=3时，求椭圆的标准方程；
2） 若
且P点横坐标为
，求面积
的最大值
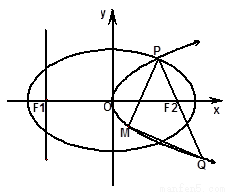
【答案】
解：（1）当m=3时，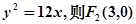
……………………………………………………1分
设椭圆方程为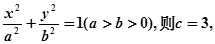
又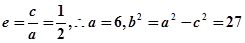
所以椭圆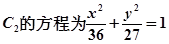
……………………………………………………4分
2）
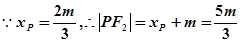
又
此时抛物线方程为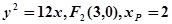
………………………………………………6分
又P在x轴上方，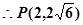
∴直线PQ的斜率为：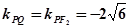
∴直线PQ的方程为：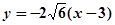
………………………………………………………8分
联立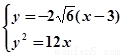 
，得
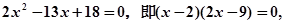
∵直线PQ的斜率为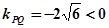
，由图知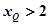
所以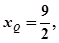
代入抛物线方程得
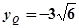，即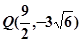
(
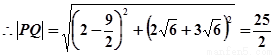
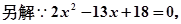
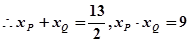
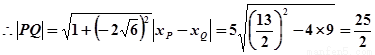)………………………………11分
设点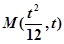
到直线PQ的距离为d,
∵M在P与Q之间运动 ,∴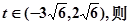 
=
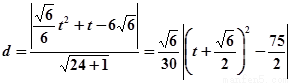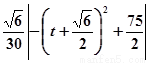
当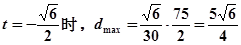
…………………………………………………14分
即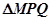
面积的最大值为
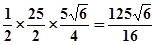…………………………………15分
【解析】略
练习册系列答案
走进文言文系列答案
相关题目
点M在y轴上，且
，点C在x轴上移动， （I）求点B的轨迹E的方程；（II）过点
的直线l与曲线E交于P、Q两点， 
的夹角为
为
中，底面
是矩形，
平面
与平面
和
，
，
依次是
的中点.
；
与平面
所成角的正弦值.
沿直线EF将
翻折成
使平面
平面BEF.
的余弦值；
重合，求线段FM的长.
的池底水平铺设污水净化管道
，
是直角顶点）来处理污水，管道越长，污水净化效果越好.设计要求管道的接口
的中点，
分别落在线段
上.已知
米，
米，记
.
表示为
的函数,并写出定义域；
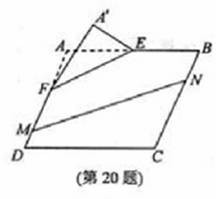本题满分15分）如图， 在矩形
中，点
分别
上，
.沿直线
翻折成
，使平面
.
的余弦值；
分别在线段
上，若沿直线
将四
向上翻折，使
与
重合，求线段