题目内容
(本题满分15分)如图,在矩形ABCD中,点E,F分别在线段AB,AD上,AE=EB=AF= 沿直线EF将
沿直线EF将 翻折成
翻折成 使平面
使平面 平面BEF.
平面BEF.
(I)求二面角 的余弦值;
的余弦值;
(II)点M,N分别在线段FD,BC上,若沿直线MN将四边形MNCD向上翻折,使C
与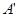 重合,求线段FM的长.
重合,求线段FM的长.

【答案】
(1) 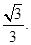
(2) 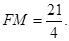
【解析】(Ⅰ)解:取线段EF的中点H,连结
因为 及H是EF的中点,
及H是EF的中点,
所以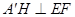
又因为平面 平面BEF,及
平面BEF,及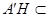 平面
平面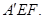
 所以
所以 平面BEF。
平面BEF。
如图建立空间直角坐标系
则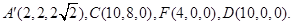
故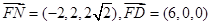
设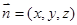 为平面
为平面 的一个法向量
的一个法向量
所以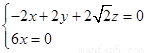
取
又平面BEF的一个法向量
故
所以二面角的余弦值为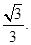
(Ⅱ)解:设
因为翻折后,C与A重合,所以CM=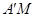
故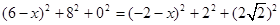 ,得
,得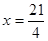
经检验,此时点N在线段BG上,所以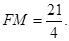

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

 中,底面
中,底面 是矩形,
是矩形, 平面
平面 与平面
与平面 和
和 ,
, ,
, 依次是
依次是 的中点.
的中点. ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 的中点,
的中点, 分别落在线段
分别落在线段 上.已知
上.已知 米,
米, 米,记
米,记 .
. 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
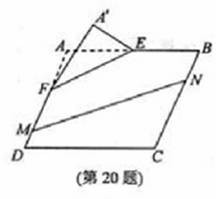 本题满分15分)如图, 在矩形
本题满分15分)如图, 在矩形 中,点
中,点 分别
分别 上,
上, .沿直线
.沿直线
 翻折成
翻折成 ,使平面
,使平面 .
.
 的余弦值;
的余弦值; 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段