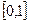题目内容
方程loga(x-ak)=loga2(x2-a2)有解时k的取值范围( )
| A.(-∞,-1)∪(0,1) | B.(-∞,-1)∪(1,+∞) | C.(0,1) | D.(-∞,0)∪(0,+∞) |
由对数性质知,原方程的解x应满足
②.
若①、②同时成立,则③必成立,
故只需解
.
由①可得2kxkx=aa(1+k2),④
当k=0时,④无解;当k≠0时,④的解是x=
,代入②得
>kk.
若k<0,则k2>1,所以k<-1;若k>0,则k2<1,所以0<kk<1.
综上,当k∈(-∞,-1)∪(0,1)时,原方程有解.
故选A.
|
若①、②同时成立,则③必成立,
故只需解
|
由①可得2kxkx=aa(1+k2),④
当k=0时,④无解;当k≠0时,④的解是x=
| a(1+k2) |
| 2k |
| 1+k2 |
| 2k |
若k<0,则k2>1,所以k<-1;若k>0,则k2<1,所以0<kk<1.
综上,当k∈(-∞,-1)∪(0,1)时,原方程有解.
故选A.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
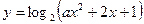 的值域为
的值域为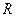 ,则
,则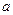 的范围为__________。
的范围为__________。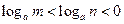 ,则
,则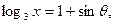 则
则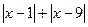 的值为 ( )
的值为 ( ) 无关
无关 ,当
,当 时的值域为( )
时的值域为( )