题目内容
8.设函数f(x)=(x-1)2+alnx,a∈R.(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-1=0垂直,求a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若函数f(x)有两个极值点x1,x2且x1<x2,求证:f(x2)>$\frac{1}{4}$-$\frac{1}{2}$ln2.
分析 (Ⅰ)先求出函数f(x)的导数,根据导函数f′(1)=2,从而求出a的值;
(Ⅱ)令g(x)=2x2-2x+a,通过讨论函数g(x)的判别式,从而得到函数f(x)的单调区间;
(Ⅲ)问题转化为求h(x)=(x-1)2+(-2x2+2x)lnx,x∈($\frac{1}{2}$,1)的单调性,得到h(x)>h($\frac{1}{2}$)=$\frac{1}{4}$-$\frac{1}{2}$ln2,从而证出结论.
解答 解:(Ⅰ)函数f(x)的定义域为(0,+∞),
f′(x)=2x-2+$\frac{a}{x}$=$\frac{{2{x^2}-2x+a}}{x}$,
∵曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-1=0垂直,
∴f′(1)=a=2.
(Ⅱ)令g(x)=2x2-2x+a,则△=4-8a.
①当△≤0,即a≥$\frac{1}{2}$时,g(x)≥0,从而f?(x)≥0,
故函数f(x)在(0,+∞)上单调递增;
②当△>0,即a<$\frac{1}{2}$时,g(x)=0的两个根为x1=$\frac{{1-\sqrt{1-2a}}}{2}$,x2=$\frac{{1+\sqrt{1-2a}}}{2}$>$\frac{1}{2}$,
当$\sqrt{1-2a}≥1$,即a≤0时,x1≤0,当0<a<$\frac{1}{2}$时,x1>0.
故当a≤0时,函数f(x)在(0,$\frac{{1-\sqrt{1-2a}}}{2}$)单调递减,在($\frac{{1+\sqrt{1-2a}}}{2}$,+∞)单调递增;
当0<a<$\frac{1}{2}$时,函数f(x)在(0,$\frac{{1-\sqrt{1-2a}}}{2}$),($\frac{{1+\sqrt{1-2a}}}{2}$,+∞)单调递增,
在($\frac{{1-\sqrt{1-2a}}}{2}$,$\frac{{1+\sqrt{1-2a}}}{2}$)单调递减.
(Ⅲ)当函数f(x)有2个极值点时,0<a<$\frac{1}{2}$,0<$\sqrt{1-2a}$<1,
此时x2=$\frac{1+\sqrt{1-2a}}{2}$∈($\frac{1}{2}$,1),且g(x2)=0,即a=-2${{x}_{2}}^{2}$+2x2,
∴f(x2)=${{(x}_{2}-1)}^{2}$+alnx2=${{(x}_{2}-1)}^{2}$+(-2${{x}_{2}}^{2}$+2x2)lnx2,
设h(x)=(x-1)2+(-2x2+2x)lnx,其中x∈($\frac{1}{2}$,1),
则h′(x)=(-4x+2)lnx,
由于x∈($\frac{1}{2}$,1)时,h′(x)>0,故函数h(x)在($\frac{1}{2}$,1)单调递增,
故h(x)>h($\frac{1}{2}$)=$\frac{1}{4}$-$\frac{1}{2}$ln2,
∴f(x2)>$\frac{1}{4}$-$\frac{1}{2}$ln2.
点评 本题考查了函数的单调性,导数的应用,考查分类讨论思想,考查函数恒成立问题,本题有一定难度.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 如图是某篮球联赛中,甲、乙两名运动员9个场次得分的茎叶图,设甲、乙两人得分平均数分别为${\overline{x}}_{甲}$、${\overline{x}}_{乙}$,中位数分别为m甲,m乙,则( )
如图是某篮球联赛中,甲、乙两名运动员9个场次得分的茎叶图,设甲、乙两人得分平均数分别为${\overline{x}}_{甲}$、${\overline{x}}_{乙}$,中位数分别为m甲,m乙,则( )| A. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,m甲<m乙 | B. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,m甲>m乙 | ||
| C. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,m甲>m乙 | D. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,m甲<m乙 |
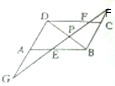 如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.
如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.