题目内容
函数
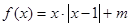
(1)设函数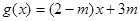 ,若方程
,若方程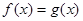 在
在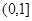 上有且仅一个实根,求实数
上有且仅一个实根,求实数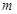 的取值范围;
的取值范围;
(2)当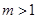 时,求函数
时,求函数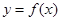 在
在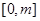 上的最大值.
上的最大值.

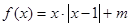
(1)设函数
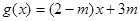 ,若方程
,若方程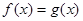 在
在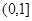 上有且仅一个实根,求实数
上有且仅一个实根,求实数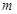 的取值范围;
的取值范围;(2)当
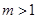 时,求函数
时,求函数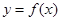 在
在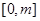 上的最大值.
上的最大值.(1)实数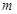 的取值范围
的取值范围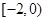
(2)当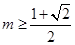 时,
时,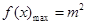 ,当
,当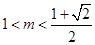 时,
时,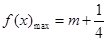
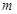 的取值范围
的取值范围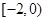
(2)当
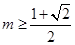 时,
时,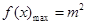 ,当
,当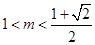 时,
时,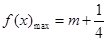
试题分析:(1)由二次方程
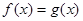 在
在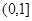 上有且仅一个实根,说明
上有且仅一个实根,说明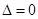 且根在
且根在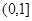 上或一根在
上或一根在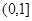 上一根不在
上一根不在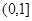 上两种情况,由以上情况列出相应关系式求实数
上两种情况,由以上情况列出相应关系式求实数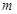
(2)当
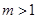 时,
时,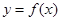 在
在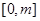 上是分段函数,分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值.
上是分段函数,分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值.试题解析:
(1)方程
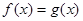 在
在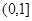 上有且仅一个实根
上有且仅一个实根即方程
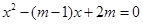 在
在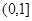 上有且仅一个实根 2分
上有且仅一个实根 2分Ⅰ当方程
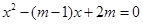 在
在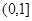 上有两个相等实根
上有两个相等实根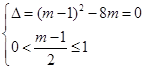 此时
此时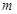 无解; 4分
无解; 4分Ⅱ当方程
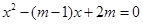 一根在
一根在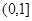 上一根不在
上一根不在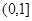 上分两类情况
上分两类情况①在
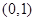 上有且仅一个实根,则
上有且仅一个实根,则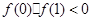
即
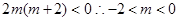 6分
6分②当
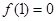 时,
时,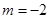 此时方程
此时方程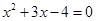
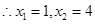 符合题意
符合题意综上所述,实数
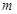 的取值范围
的取值范围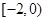 8分
8分(2)Ⅰ当
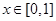 时,
时,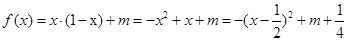
∴当
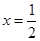 时,
时,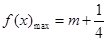 10分
10分Ⅱ当
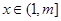 时,
时,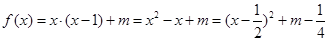
∵函数
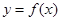 在
在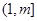 上单调递增
上单调递增∴
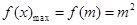 12分
12分由
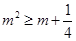 得
得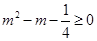 又
又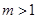
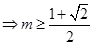
∴当
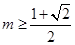 时,
时,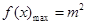 ,当
,当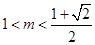 时,
时,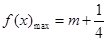 . 14分
. 14分
练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
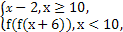 则f(5)的值为( )
则f(5)的值为( )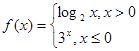 ,则
,则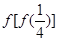 的值是 .
的值是 .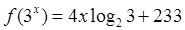 ,则
,则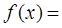
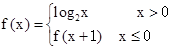 ,则
,则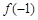 =__________.
=__________.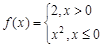 ,则满足
,则满足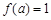 的实数
的实数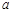 的值为 .
的值为 .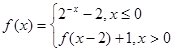 ,则
,则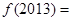 .
.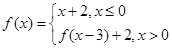 ,则
,则 .
.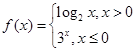 ,则
,则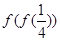 的值是 .
的值是 .